MEDP_Información general

Bienvenida

Bienvenido(a) a la unidad didáctica Ecuaciones diferenciales parciales, en la cual trabajarás con diferentes actividades que te ayudarán a desarrollar habilidades y concretar los objetivos de aprendizaje propuestos en la unidad didáctica, a través del trabajo individual y colaborativo.

Fuente: Imagen extraída de https://n9.cl/jvsw23

Se trata de un primer curso sobre soluciones clásicas de cierto tipo de Ecuaciones Diferenciales Parciales (EDP), donde, en la Unidad 1, se comienza por exponer los conceptos básicos de la teoría, se explica qué son las EDP y cómo se plantean los problemas de contorno y con condiciones iniciales. En particular, se deducen las ecuaciones fundamentales y el planteamiento de los problemas con condiciones iniciales y de contorno para los procesos de difusión del calor y propagación de ondas, así como los correspondientes modelos estacionarios que conducen al estudio de problemas de contorno para las ecuaciones de Laplace y Poisson.

En la Unidad 2 se efectúa la clasificación principal de las ecuaciones cuasilineales de segundo orden en elípticas, parabólicas e hiperbólicas, y se estudia el problema de Cauchy sobre una superficie no característica para estas ecuaciones cuando la variable espacial está dada en todo Rⁿ.

La Unidad 3 se dedica al estudio del problema de contorno de Dirichlet para la ecuación de Laplace, para lo cual se introduce la noción fundamental de función de Green y también al estudio de los problemas mixtos para la ecuación del calor y la ecuación de ondas, utilizando el método de separación de variables y el método de superposición que consiste en representar las soluciones de estos problemas en forma de series de Fourier.

Da clic en el ícono, para descargar la Información general de la unidad didáctica.

Da clic en Competencias y logros para continuar con la revisión de la información general.

Competencias y logros

Competencia general

Resolver problemas con condiciones iniciales, de contorno y mixtos, tanto en todo Rⁿ como en regiones acotadas con geometría simple, de ecuaciones diferenciales, parciales, lineales y cuasilineales de primer orden, así como ecuaciones lineales de segundo orden, para interpretar físicamente los resultados de las soluciones matemáticas de los principales problemas de contorno asociados a las ecuaciones básicas de la física matemática, mediante métodos clásicos del análisis funcional y de las EDP.

Da clic en cada pestaña para revisar las competencias y logros que alcanzarás en esta unidad didáctica.

Competencia específica

Aplicar las ecuaciones básicas de la física matemática y plantear los problemas de contorno asociados a ellas, para resolver problemas prácticos que puedan ser modelados por tales ecuaciones, mediante la vinculación y generalización de los conceptos y resultados de Álgebra Lineal, Análisis Matemático y EDO.

Logros:

Clasificar algunas de las EDP de acuerdo a las propiedades que tienen.
Plantear el problema de Cauchy en los diferentes órdenes.
Determinar métodos de solución para el problema de Cauchy.

Competencia específica

Obtener las soluciones del problema de Cauchy para las ecuaciones de onda y de calor en dimensiones uno, dos y tres; mediante la aplicación de las fórmulas correspondientes, para resolver los modelos asociados a problemas clásicos de la física matemática.

Logros:

Clasificar las EDP cuasilineales de segundo orden de acuerdo a su reducción a la llamada forma canónica.
Presentar el llamado problema de Cauchy para una EDP cuasilineal de segundo orden y estudiar su relación con la noción de superficie característica y la clasificación vista previamente.
Presentar un planteamiento particular para el problema de Cauchy para la ecuación de ondas y estudiar las propiedades de su solución de acuerdo a la dimensión espacial.
Presentar un problema particular con condiciones iniciales para la ecuación de calor que puede ser considerado como una generalización del problema de Cauchy.

Competencia específica

Utilizar los resultados de la teoría asociada a los problemas de Sturm-Liouville y Dirichlet, la teoría de las series de Fourier y las propiedades de las funciones armónicas, para resolver EDP con condiciones de contorno y mixtos además de analizar el comportamiento de potenciales de campos ideales, mediante fórmulas de representación por medio de la función de Green y el método de separación de variables.

Logros:

Presentar el método de la función de Green y el método de separación de variables como métodos fundamentales para el estudio de los problemas de contorno asociados al operador de Laplace en una región acotada, haciendo énfasis en el problema de Dirichlet.
Desarrollar métodos de cálculo de la función de Green del problema de Dirichlet para la ecuación de Laplace en algunas regiones con simetría.
Presentar el método de separación de variables combinado con el método de superposición de Fourier para el estudio de problemas mixtos asociados a las ecuaciones de calor y de ondas, fundamentalmente en el caso de una dimensión espacial.

Da clic en Temario para continuar con la revisión de la información general.

Temario

El contenido que estudiarás en cada unidad de este módulo se presenta a continuación.

Da clic en cada unidad para ver los temas y subtemas.

Unidad 1. Ecuaciones diferenciales parciales

1.1. Definiciones principales

1.1.1. ¿Qué son y cómo surgen las EDP?

1.1.2. Los operadores GRAD, ROT; DIV y Laplaciano

1.1.3. Problemas con condiciones iniciales y de contorno asociados a las EDP

1.2. Ejemplos clásicos de EDP de a física matemática y significado de los problemas de contorno asociados a las EDP

1.2.1. Ecuación de la difusión:la ecuación del calor

1.2.2. Ecuaciones de la cuerda y la membrana vibrantes

1.2.3. Ecuaciones estacionarias y ecuaciones para los potenciales de campos ideales: las ecuaciones de Laplace y Poisson

1.2.4. Ecuaciones de Maxwell: la ecuación de ondas

1.2.5. Ecuaciones de primer orden: conservación de masa, Euler y las ecuaciones de la mecánica de fluidos

1.3. EDP de primer orden y su relación con las EDO: el problema de Cauchy

1.3.1. EDP lineales y cuasilineales de primer orden

1.3.2. El problema de Cauchy

1.3.3. Método de las características y soluciones generales

Unidad 2. El problema de Cauchy para EDP de segundo orden

2.1. Clasificación de las EDP cuasilineales de segundo orden

2.1.1. El problema de Cauchy para algunos ejemplos e EDP de segundo orden

2.1.2. Formas canónicas y clasificación

2.1.3. Problema de Cauchy y superficies características

2.2. El problema de Cauchy para la ecuación de onda en dimensiones espaciales uno, dos y tres

2.2.1. La ecuación de onda en dimensión uno: la fórmula de D’Alembert

2.2.2. La ecuación de onda en dimensión espacial tres: método de las medias esféricas

2.2.3. El problema de Cauchy en dimensión espacial dos: método de descenso de Hadamard

2.2.4. La ecuación de onda no homogénea

2.2.5. Energía y unicidad de solución del problema de Cauchy

2.2.6. Propiedades de la solución de la ecuación de onda de acuerdo a la dimensión espacial

2.3. El problema de Cauchy para la ecuación de calor

2.3.1. Núcleo de Gauss. Solución del problema de Cauchy

2.3.2. El principio del máximo. Resultados clásicos de unicidad

2.3.3. Comparación entre las soluciones del problema de Cauchy para la ecuación de onda y la ecuación de calor

Unidad 3. Problemas de contorno y problemas mixtos para EDP de segundo orden

3.1. Problemas de contorno para la ecuación de Laplace en una región acotada

3.1.1. El teorema de divergencia y la fórmula de Green. Condición necesaria para la solución del problema de Neumann

3.1.2. Solución fundamental del operador de Laplace y representación integral de funciones

3.1.3. El problema de Dirichlet para el operador de Laplace en una bola de 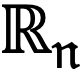y su función de Green

3.1.4. Cálculo de la función de Green en dominios con simetrías: semiespacios

3.1.5. Propiedades de las funciones armónicas

3.1.6. La ecuación de Poisson

3.2. Problema de Stum-Liouville. Series de Fourier

3.2.1. Sistemas de vectores linealmente independientes, ortogonales y bases ortonormales. Bases formadas por vectores propios de operadores lineales y series de Fourier.

3.2.2. Principio de superposición para resolver ecuaciones lineales

3.2.3. El problema de Sturm-Liouville autoadjunto. Teorema de alternativa y función de Green

3.2.4. Autovalores y autovectores del problema de Sturm-Liouville autoadjunto. Completitud de los vectores y series de Fourier

3.3. El método de separación de variables para resolver problemas mixtos

3.3.1. Problemas mixtos para la ecuación de calor en una dimensión espacial

3.3.2. Problemas mixtos para la ecuación de onda: caso de la cuerda vibrante

3.3.3. El problema de Dirichlet para la ecuación de Laplace en un cuadrado y disco unitario en el plano

Da clic en Metodología de trabajo para continuar con la revisión de la información general.

Metodología

Al revisar los contenidos de esta unidad didáctica, identificarás las definiciones básicas para las ecuaciones diferenciales parciales, para comprender y plantear los problemas de la física matemática.

En cada una de las unidades, con el auxilio de los contenidos presentados, resolverás ejercicios y problemas que te brindarán una visión más amplia sobre los problemas de la física matemática con las ecuaciones diferenciales parciales.

La metodología que se ha diseñado para trabajar a lo largo de estas unidades es del tipo Aprendizaje basado en ejercicios y problemas, en el que se te plantearán diferentes situaciones usando los conceptos que se vayan revisando para ponerlos en práctica. Los problemas y ejercicios planteados corresponden a todo lo que se haya visto hasta ese momento en la unidad y, de la misma forma, lo que se haya visto en unidades anteriores, según aplique el caso.

Durante las tres unidades se te brindarán actividades colaborativas, foros, tareas y una evidencia de aprendizaje que permitirá medir el grado de conocimiento adquirido durante cada una de los temas fundamentales.

Da clic en Evaluación para continuar con la revisión de la información general.

Evaluación

La evaluación del aprendizaje es un proceso, a través del cual se observa, recoge y analiza información relevante del proceso de aprendizaje de los estudiantes, con la finalidad de reflexionar, emitir juicios de valor, así como tomar decisiones pertinentes y oportunas para optimizarlo (Díaz Barriga A.F. & Hernández R.G., 2005). Orienta la toma de decisiones, da pauta a determinar acciones en términos de valoración de conocimientos, nivel del desempeño, reorientaciones de aprendizaje, mejora del proceso educativo y adecuación de actividades, entre otras acciones.

De acuerdo con lo anterior, mediante la evaluación te brindaremos apoyo y seguimiento para identificar las dificultades en el desarrollo de conocimientos, habilidades y actitudes del proceso integral de aprendizaje.

En el marco del Modelo educativo de la UnADM, la evaluación de la unidad didáctica se realiza en los siguientes momentos:1) formativa y 2) sumativa.

Evaluación formativa

Se realiza en paralelo al desarrollo del proceso de enseñanza-aprendizaje de cada unidad, y sirve para localizar dificultades cuando aún estás en posibilidad de remediarlas.

En este primer momento de evaluación, se aplican estrategias asociadas a las:

Actividades individuales (tareas). Se trata de un primer momento de aprendizaje, en el cual se consideran tus perspectivas, experiencias, intereses, capacidades y necesidades.
Actividades colaborativas (foros). El trabajo colaborativo fomenta y promueve el aprendizaje en contribución con otros compañeros, ya que eres responsable no sólo de tu aprendizaje, sino de contribuir a que los demás aprendan en equipo y se fomente un ambiente de confianza; por ende, que se logren las metas de aprendizaje.

Evaluación sumativa

Se aplica al final del proceso de tu experiencia de aprendizaje, su propósito es verificar los resultados alcanzados y el grado de aprendizaje o nivel de conocimientos, habilidades y actitudes que hayas adquirido.

Este segundo y último momento de evaluación, se mide y valora a través de las siguientes actividades:

Evidencias de aprendizaje. Son actividades que tienen como objetivo integrar el proceso de construcción de tu aprendizaje, la evaluación, la retroalimentación y la planeación de la nueva ruta de aprendizaje que seguirás de acuerdo con los resultados individuales obtenidos.
Actividad complementaria. Esta actividad es planeada por la figura académica considerando las competencias y logros de la unidad didáctica, toda vez que identifica los conocimientos, habilidades y actitudes que te hizo falta desarrollar o potenciar (se realiza en una ocasión al finalizar la última unidad).

A continuación, se presenta el esquema general de evaluación correspondiente a esta unidad didáctica:

Tipo de evaluación	Tipo de aprendizaje	Puntaje
Formativa	Actividades individuales	35
Formativa	Actividades colaborativas	10
Sumativa	Evidencias de aprendizaje	45
Sumativa	Actividad complementaria	10
Total		100

Recuerda que la calificación final que te permitirá acreditar, se asigna de acuerdo con los criterios e instrumentos de evaluación establecidos para cada actividad, los cuales son diseñados con base en las competencias y logros de esta unidad didáctica.

Da clic en Fuentes de consulta para continuar con la revisión de la información general.

Fuentes de consulta

Básica

Aguilar-Loreto, Omar y Muñoz-Gómez, José A. 2016 (). Ecuaciones diferenciales parciales, 1.ª ed. Guadalajara, México: Editorial Universidad de Guadalajara. México. https://editorial.udg.mx/gpd-ecuaciones-diferenciales-parciales.html.
Bgchi, B. k. (2020). Partial differential equations for mathematical physicists. CRC Press.
Cengel, Yunus (2013) Ecuaciones diferenciales para ingeniería y ciencias. MacGraw-Hill Interamericana de España S.L.
Fernández-Bonder, Julián. (2015). Ecuaciones Diferenciales Parciales, Universidad de Buenos Aires, Argentina. https://cms.dm.uba.ar/depto/public/grado/fascgrado7.pdf.
Giardano, Claudia M. (2017). Ecuaciones diferenciales parciales. Universidad Nacional de La Plata. Argentina.
Henner,V., Belozerova, T., Nepomnyashchy, A. (2020). Partial differential equations: Analytical methods and applications. CRC Press.
Ireneo P. A. (S.f.). Ecuaciones en Derivadas Parciales. Universidad Autónoma de Madrid. España.
Weinberger, Hans F. (2005). Ecuaciones Diferenciales en Derivadas Parciales. Ed. Reverte. España.

Muy bien, has concluido la revisión de la Información general, ahora inicia el estudio de la unidad 1.