Cuando se estudia un conjunto de datos que constituye una muestra de una población, comúnmente la organización y la descripción de los datos no es la finalidad principal. El aspecto de más importancia es la derivación de conclusiones que involucran características de toda la población de donde se extrajo la muestra. Sin embargo, debe tenerse presente que, dado que este tipo de conclusiones está basado en el análisis de sólo una parte de la población a caracterizar, siempre existirá la posibilidad de cometer errores al concluir hacia el todo con base en el análisis de una parte. Una de las contribuciones importantes de la Estadística al avance científico es, precisamente, permitir que la incertidumbre de este tipo de conclusiones pueda ser evaluada en términos de probabilidad.

La probabilidad es importante no sólo por expresar los grados de credibilidad inherentes a los procesos típicos de inferencia estadística. Muchas ciencias hacen un uso muy importante de la probabilidad para expresar los grados de confiabilidad de la ocurrencia de eventos de interés. Así, por ejemplo, podría ser interesante establecer, en términos probabilísticos, el grado de confiabilidad de que llueva mañana o de que un individuo por nacer sea de un genotipo particular.

La probabilidad es una rama de las matemáticas cuyas raíces se encuentran en los juegos de azar. Así, muchos de los ejemplos que se utilizan para ilustrar problemas de probabilidad tienen que ver con lanzamientos de dados y juegos de naipes.

Para establecer una definición de sencilla e intuitiva de probabilidad, comenzaremos con un ejemplo: supongamos que hay cuatro canicas en un costal, tres son negras y una blanca. Sacudimos vigorosamente el costal y luego, con los ojos cerrados, sustraemos una canica. Ahora nos preguntamos: ¿cuál es la probabilidad de que la canica sustraída sea negra? Supongamos que la respuesta será algo como “tres de cuatro” o “tres cuartos” o “punto setenta y cinco”.

Concordamos con estas respuestas, pero ¿qué definición de probabilidad se utilizó para llegar a la respuesta? Si reflexionamos un poco, nos daremos cuenta de que se definió la probabilidad de sustraer una canica negra como el número de canicas negras dividido entre el número total de canicas. ¿Cuál es la probabilidad de que la canica sea blanca? De nuevo, la probabilidad es simplemente el número de canicas blancas dividido entre el número total de canicas.

Formalmente, podemos definir la probabilidad de algún suceso, llamémosle A, como:

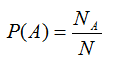
El símbolo P() se lee “La probabilidad de…”, donde A se usa para representar cualquier suceso de interés, como sacar una canica blanca.

Se utilizará el símbolo à para referirse al complemento de A, que en este caso significaría “no sustraer una canica blanca”.

Así, en el caso que nos ocupa, P(Ã) se leería: “La probabilidad de no extraer una canica blanca”. Por su parte, N_A es el número de eventos que cumplen el criterio especificado y N es el número total de eventos.

Se pueden deducir varias propiedades importantes a partir de la definición de probabilidad establecida a partir de la ecuación anterior:

Da clic en el tema 1.2. Probabilidad de la unión de dos eventos para revisar el contenido.

La probabilidad de la unión de dos eventos se calcula por medio de la siguiente ecuación:

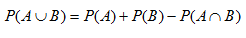
Donde A y B son dos eventos de un espacio muestral determinado. De esta forma, la probabilidad de la unión de dos eventos, A y B, es igual a la suma de las probabilidades de ambos eventos, menos la probabilidad de la ocurrencia de ambos eventos simultáneamente.

Esta expresión nos indica que, para calcular la probabilidad de la unión de dos eventos, se descarta la probabilidad de que sucedan ambos simultáneamente, en el caso de que exista esa posibilidad.

En esta situación los eventos no son excluyentes porque existe la posibilidad de que sucedan simultáneamente. Por ejemplo, si en un conjunto de autos, el evento A es el conjunto de todos los autos de dos puertas y el evento B es el conjunto de todos los autos de color rojo, entonces A ∩ B sería el conjunto de todos los autos de dos puertas y que son rojos.

Si queremos saber la probabilidad de encontrar el conjunto de automóviles que son de dos puertas o que son rojos, se tiene que calcular primero la probabilidad de encontrar autos de dos puertas, después calcular la probabilidad de encontrar autos de color rojo y, finalmente, la probabilidad de encontrar autos de dos puertas y de color rojo.

Si no existen autos de dos puertas y de color rojo, entonces la ecuación anterior se reduce a:

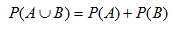
En el caso de que no existan autos de dos puertas y que sean de color rojo, se dice que son eventos mutuamente excluyentes. La ecuación anterior calcula la probabilidad de que suceda A o que suceda B para eventos excluyentes o independientes.

Por ejemplo, supongamos que en un lote existen 50 autos, de los cuales 15 son autos de dos puertas, 10 son autos de color rojo y 5 son autos de dos puertas de color rojo. La probabilidad de encontrar un auto de dos puertas o un auto de color rojo, es igual a:

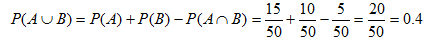
Es decir, existe el 40% de probabilidad de escoger, en ese lote de autos, un auto que es de dos puertas o es de color rojo.

Si no existen autos de dos puertas y son de color rojo, entonces la probabilidad de obtener un auto de dos puertas o de color rojo, es igual a:

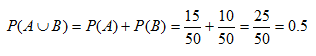
En consecuencia, para eventos excluyentes no existe la probabilidad de que sucedan ambos simultáneamente.

Da clic en el tema 1.3. Probabilidad condicional para revisar el contenido.

La probabilidad condicional está relacionada con la probabilidad de que suceda un evento B , dado que sucedió otro evento A. Esta probabilidad se representa como:

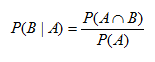
Donde:

P(B|A) es la probabilidad de que suceda B dado que sucedió A; P(A ∩ B) es la probabilidad de que sucedan los dos eventos simultáneamente y P(A) es la probabilidad de que suceda el evento A.

En consecuencia, la probabilidad de que suceda el evento A y el evento B simultáneamente se expresa de la siguiente manera:

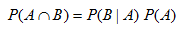
Como ejemplo, supongamos que se quiere encontrar la probabilidad de que dos tornillos que se extraigan al azar no estén defectuosos, de un conjunto de 10 tornillos de los cuales 3 están defectuosos.

La probabilidad de que se extraiga un tornillo no defectuoso es igual a:

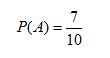
Y la probabilidad de que se extraiga el siguiente tornillo que no esté defectuoso, es igual a:

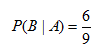
Se utiliza 6 en el numerador porque ya se ha extraído un tornillo no defectuoso y 9 porque sólo quedan 9 tornillos. En consecuencia, la probabilidad de que se extraigan dos tornillos no defectuosos, es igual a:

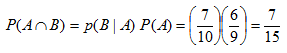
Da clic en Actividad de aprendizaje para realizar la actividad.

Da clic en el tema 1.4. Distribución discreta de probabilidad para revisar el contenido.

Los modelos de probabilidad discretos se describen por medio de su función de probabilidad.

La función de probabilidad de una variable aleatoria discreta es una función que, a cada posible valor de la variable aleatoria, le asigna la probabilidad de obtener dicho valor cuando se realiza una observación.

Los modelos discretos de probabilidad se utilizan para describir ciertos experimentos, por ejemplo, el modelo binomial, que es ampliamente usado en el control de calidad en la industria, la medicina, la electrónica, entre otras industrias. El modelo de Poisson se utiliza para la modelación del comportamiento de filas o líneas de espera. En esta sección se trabajará los modelos discretos más usuales, sus funciones de distribución, parámetros asociados, su esperanza y varianza.

Da clic en el subtema 1.4.1. Distribución Bernoulli para revisar el contenido.

El modelo de Bernoulli es uno de los más simples. Un experimento aleatorio es de tipo Bernoulli cuando sólo tiene dos resultados posibles, y generalmente dichos valores están asociados a “éxito” y “fracaso”. Por ejemplo, al lanzar una moneda (balanceada) al aire, los posibles resultados son “águila” y “sol”; por eso, el lanzamiento de una moneda es un experimento de tipo Bernoulli, a diferencia de lanzar un dado, ya que este experimento tiene 6 posibles resultados.

Sea X una variable aleatoria definida en el experimento tipo Bernoulli, la cual representa el éxito en el experimento, generalmente los valores de X son 0 y 1, esto es R_X = {0,1}.

Definición. Sea un parámetro 0 < p < 1. La X es una variable aleatoria que tiene función de probabilidad (o distribución) Bernoulli, denotada X~Ber(p), definida como:

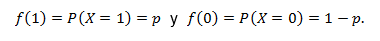
En general, se toma que q = (1 - p), entonces es fácil determinar la esperanza y varianza de una variable aleatoria (va) X~Ber(p).

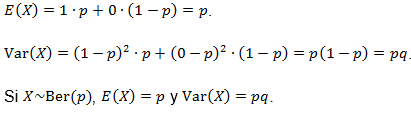
Da clic en el subtema 1.4.2. Distribución binomial para revisar el contenido.

El modelo binomial es empleado en situaciones donde nos interesa conocer una suma de éxitos o una proporción en una población. Este modelo se basa en un número de repeticiones del experimento de tipo Bernoulli.

Un experimento aleatorio se llama binomial cuando se cumplen las siguientes condiciones:

• El experimento consta de n (un número finito) de ensayos en forma idéntica.
• Cada ensayo tiene dos posibles resultados: éxito o fracaso, tipo Bernoulli.
• Los ensayos son independientes, es decir, el resultado de un ensayo no depende de los ensayos anteriores.
• La probabilidad de éxito en cada prueba es p y la probabilidad de fracaso es q = (1-p); ambas se mantienen constantes en cada prueba.
• La variable aleatoria en el experimento describe el número de éxitos en los n ensayos.

Observa que los valores que puede tomar la variable X son 0, 1,2,…,n.

Definición. Sean n ∈ N, 0 < p < 1 y q = (1 - p). La variable aleatoria X tiene función de probabilidad (o distribución) binomial con parámetros n y p, denotada X~Bin(n,p), definida como:

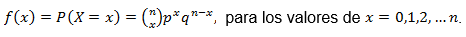
Ejemplo: supongamos que 20% de todas las computadoras producidas por una compañía necesitan un servicio durante su periodo de garantía. Sea X el número de computadoras, entre 15 seleccionadas aleatoriamente que necesitarán un servicio. Entonces, si X tiene una distribución binomial con n = 15 y p = 0.2:

Da clic en el subtema 1.4.3. Distribución geométrica para revisar el contenido.

En la práctica, con frecuencia se tienen experimentos también de ensayos independientes, pero a diferencia de los binomiales no tienen una cantidad finita para realizarse, sino que el experimento termina hasta obtenerse el primer éxito, lo cual no necesariamente podría darse. A estos modelos se les conoce como modelos geométricos. Por ejemplo, al lanzar una moneda balanceada sea la v. a. tal que X: la cantidad de lanzamientos hasta la primera águila; obviamente, los posibles valores que puede tomar X serán 0, 1, 2, 3,…, n,...

Definición: Sean 0 < p < 1 la probabilidad de éxito y q = (1 - p) la probabilidad de fracaso. La variable aleatoria X tiene función de probabilidad (o distribución) geométrica con parámetros n y p, denotada X~Geo(p), definida como:

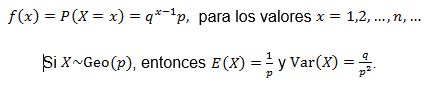
Da clic en el subtema 1.4.4. Distribución de Poisson para revisar el contenido.

El modelo Poisson se utiliza en experimentos cuyos resultados tienen lugar en intervalos continuos de tiempo. Sin embargo, el modelo es discreto, puesto que nos interesará la cantidad de resultados que pueden ocurrir en un intervalo de tiempo dado, mas no la continuidad del intervalo. Este modelo se utiliza para optimizar tiempos, tanto de espera como de servicios. A estas investigaciones se les conoce como líneas de espera o teoría de colas.

Ejemplos:

• Un departamento de atención a clientes desea estimar el promedio de llamadas por hora. Entendemos por número de llamadas la suma de ocurrencias en un espacio de tiempo de una hora.
• Un laboratorio de análisis clínicos realiza estudios en los que requiere contar el número de ocurrencias de plaquetas, leucocitos, neutrófilos, linfocitos, etc., por ml², con el fin de estimar el promedio de ocurrencias por unidad de volumen.
• Un supermercado está interesado en observar el promedio de clientes que llega a las cajas por hora.
• El departamento de tránsito está interesado en estimar el promedio de accidentes por semana en un crucero peligroso.

Un experimento aleatorio de Poisson tiene las siguientes características:

• λ es un parámetro de la población y se conoce como el promedio de ocurrencias por unidad específica (de tiempo, área o volumen).
• El promedio de ocurrencias por unidad específica es proporcional al tamaño (o longitud) de la unidad.
• Los resultados de intervalos que no tienen puntos en común son independientes.
• La variable aleatoria asociada al experimento es el número de ocurrencias por una unidad específica.

Por ejemplo, en la Ciudad de México suelen ocurrir sismos de vez en cuando; sin embargo, el número de ocurrencias de un sismo en un intervalo de tiempo breve (una hora o un día) es pequeño (casi despreciable). Pero podría decirse que, en promedio, ocurren tres sismos cada lustro, es decir en este caso λ = 3.

Definición. Sea 0 < λ un parámetro. La variable aleatoria X tiene función de probabilidad (o distribución) de Poisson con parámetro λ, denotada X~Poisson(λ), definida como:

Da clic en el tema 1.5. Distribución continua de probabilidad para revisar el contenido.

Los modelos de probabilidad continuos se describen por medio de su función de densidad.

La función de densidad de una variable aleatoria continua es una curva situada encima del eje de las abscisas, que a cada intervalo de posibles valores de la variable aleatoria le asigna la probabilidad determinada por el área que dicha curva encierra con el eje de abscisas en ese intervalo.

Los modelos continuos de probabilidad se utilizan para describir ciertos experimentos, por ejemplo, el modelo normal es ampliamente usado para las mediciones físicas en áreas como los experimentos meteorológicos, estudios de lluvia y mediciones de partes fabricadas, entre otros. El modelo exponencial se utiliza para describir fenómenos relacionados con tiempo de vida. El modelo t-Student es utilizado cuando se desea hacer una inferencia en una muestra pequeña. En este tema se trabajarán los modelos continuos más usuales: sus funciones de distribución, parámetros asociados, su esperanza y varianza.

Da clic en el subtema 1.5.1. Distribución uniforme continua para revisar el contenido.

El modelo uniforme continuo es uno de los más sencillos, ya que se caracteriza porque su distribución es igual en todos los puntos de un segmento, y debido a esto se emplea en la simulación para el cálculo de números aleatorios con un comportamiento uniforme.

Definición. Una variable aleatoria X tiene distribución uniforme continua en un intervalo (a,b), denotada X~U(a,b), si su función de densidad es:

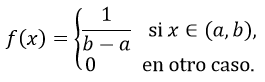
Cabe mencionar que en muchos libros de texto encontrarás que dicha distribución uniforme se define para el intervalo cerrado [a,b], sin embargo, aquí se define para el intervalo abierto (a,b). Recuerda que para una v.a. continua la probabilidad en puntos es nula, por lo cual la definición no resulta afectada si es con uno u otro intervalo.

Teorema: Si X es una variable aleatoria con distribución uniforme en (a,b), X~U(a,b), entonces:

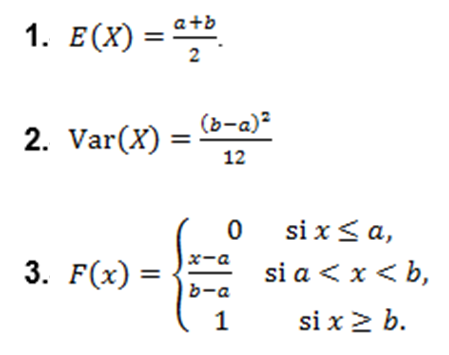
Todo lo anterior es fácilmente demostrable.

Las siguientes gráficas corresponden a la función densidad y distribución uniforme (Figura 1.1).

Figura 1.1. Función de densidad y distribución uniforme

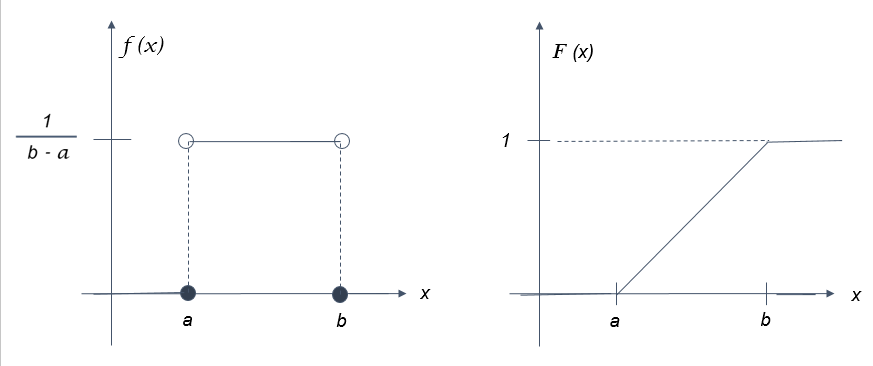
Observa que el área por debajo de la función f(x) es un rectángulo con altura 1/(b-a) y base b - a, por lo que su área es 1.

Ejemplo: Estimar el peso de una persona siempre presenta márgenes de error que dependen del tipo báscula, y estos errores pueden variar por gramos o hasta algunos kilos. Considera una báscula digital que nos garantiza un error de entre 0 y 1000 g. ¿Qué probabilidad hay de que el peso real exceda 500 g?

Si la distribución del error es uniforme en el intervalo (0,1000), entonces la función de densidad queda representada por la función f(x), con una altura de 1/1000.

La probabilidad se calcula integrando el área debajo de f(x) en el intervalo (500,1000); por observación, sabemos que esta área es igual a 0.5 si usamos:

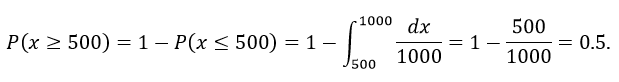
Da clic en el subtema 1.5.2. Distribución exponencial para revisar el contenido.

Esta distribución es comúnmente utilizada en los modelos de líneas de espera, al igual que la distribución discreta de Poisson. De hecho, éstas tienen una relación muy estrecha. En la mayoría de los modelos relacionados con el tiempo, se puede notar que su distribución es tal que en tiempos pequeños (cercanos a cero) tienen una mayor acumulación (o área), y conforme pasa el tiempo ésta decrece rápidamente.

Definición. Una variable aleatoria X tiene distribución exponencial con parámetro λ > 0, denotada X~Exp(λ), si su función de densidad es:

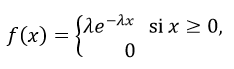
Teorema. Si X es una variable aleatoria con distribución exponencial y con parámetro λ > 0, X~Exp(λ), entonces:

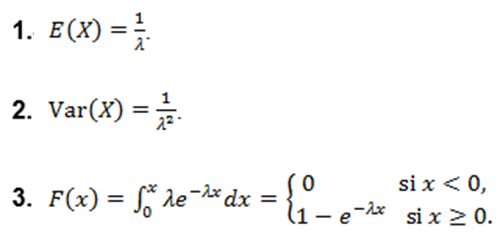
Las siguientes son las respectivas gráficas de densidad y distribución de X~Exp(λ=3) (Figura 1.2):

Figura 1.2. Densidad de distribución X~Exp(λ=3)

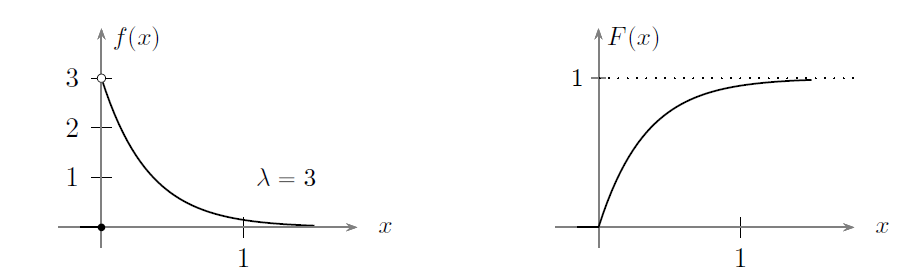
Da clic en el subtema 1.5.3. Distribución X² (chi o ji cuadrada) para revisar el contenido.

Esta distribución es de importancia en las aplicaciones de diferentes metodologías estadísticas. Guarda relación con los estadísticos 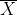y σ ², asociados a muestras aleatorias obtenidas de poblaciones normales: es decir, si X₁, X₂,...,X_n son una muestra aleatoria de una población normal, la distribución X² tiene relación con los estadísticos:

Se dice que una variable continua Y sigue una distribución X² con m grados de libertad si su función de densidad de probabilidades es de la forma:

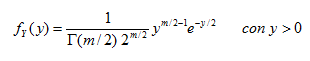
En donde: 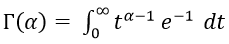y se le conoce como función gamma.

Dado lo complejo de la función de densidad de probabilidades de una variable aleatoria que sigue una distribución chi cuadrada, para el cálculo de probabilidades de eventos que involucran esta variable aleatoria, se han elaborado tablas para chi cuadrada para diferentes grados de libertad. De igual forma, se pueden calcular los valores de chi cuadrada por medio de hojas de cálculo como Excel.

Por ejemplo, se puede pedir las probabilidades de los siguientes valores:

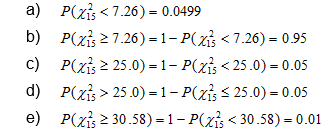
Para obtener estos resultados a través de Excel, en una celda se debe escribir lo siguiente: =DISTR.CHICUAD(7.26,15,VERDADERO). Al oprimir la tecla de retorno o enter, el resultado de la operación sería igual a 0.0499.

Por ejemplo, para una variable Y tal que 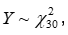, encuentra los valores de c y a, tales que:

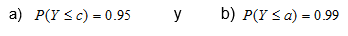
Utilizando la función inversa de chi cuadrada, se tiene =INV.CHICUAD(0.95,30), por lo que el valor de c es igual a 43.8. De igual forma, utilizando la función inversa de chi cuadrada, se tiene =INV.CHICUAD(0.99,30), por lo que el valor de a es igual a 50.89.

Da clic en el subtema 1.5.4. Distribución t-Student para revisar el contenido.

Los cálculos probabilísticos de la ocurrencia de eventos relacionados con las distribuciones normal y ji-cuadrada fueron posibles gracias a que se referían a casos hipotéticos de distribuciones normales de ciertos parámetros conocidos. En los problemas de la realidad asociados con distribuciones normales, los parámetros de dichas distribuciones son típicamente desconocidos. La solución a este problema se encuentra mediante el uso de la distribución t-Student. El descubrimiento de esta distribución ha significado una de las mayores contribuciones que se han hecho a la estadística.

Su utilidad es importante porque se aplica en problemas de estimación y pruebas de hipótesis relacionados con parámetros de distribuciones normales.

La función de densidad de probabilidad está dada por la siguiente ecuación:

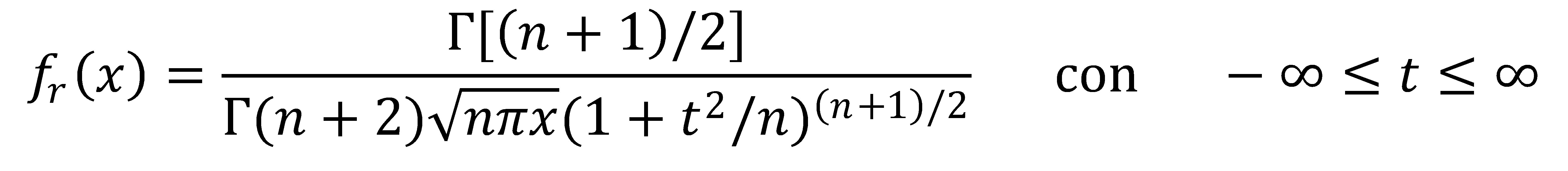
Donde: n son los grados de libertad y Γ es la función gama.

A medida que los grados de libertad aumentan, la forma de la distribución se asemeja más a la forma de la distribución normal. De igual forma, la distribución t-Student es simétrica, cuyo eje de simetría se encuentra en t = 0.

Como ejemplo, calculemos t _{0.99, 20} , es decir, el valor de t para el cual se encuentra hasta el 99% de la distribución t-Student con 20 grados de libertad. Esto significa que buscamos un punto en el eje tal que a mano izquierda del mismo y bajo la curva haya el 99% del área total. Utilizando una hoja de cálculo como Excel, se debe escribir lo siguiente: =INV.T(0.99,20), cuyo resultado es igual a t = 2.527977.

Se utiliza la función inversa, ya que se quiere conocer el valor de t para el cual exista el 99% del área bajo la curva de la función de distribución.

Si quisiéramos saber la probabilidad de que t = 2 con 20 grados de libertad, debemos utilizar la función de densidad de t-Student. Para ello empleamos una hoja de cálculo como Excel e introducimos estos datos en la siguiente función:

=DISTR.T.N(2,20,VERDADERO).

Al introducir esta instrucción, vemos que la probabilidad de obtener un valor de t = 2 con 20 grados de libertad es igual a 0.970367, que corresponde al 97% de probabilidad, aproximadamente.

Da clic en el subtema 1.5.5. Distribución normal para revisar el contenido.

El modelo normal es considerado como uno de los más importantes en el estudio de la probabilidad y la estadística. Esto se debe a que la gran mayoría de fenómenos tiene un comportamiento que se describe apropiadamente mediante este modelo.

La distribución normal fue estudiada por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) profundizó en el desarrollo de lo que actualmente conocemos como “campana de Gauss”, la cual es usada como función de densidad de la distribución normal.

La distribución de probabilidad normal se considera la distribución más importante en inferencia estadística. Ésta requiere de muestras aleatorias seleccionadas de una población para estimar algunas características numéricas que se llaman parámetros. Ejemplos de parámetros son la μ (media), la proporción de éxitos (p), la comparación de dos poblaciones (diferencia de medias: μ₁- μ₂) o la diferencia de proporciones p₁- p₂.

La distribución de una variable normal está completamente determinada por dos parámetros, su media μ y su desviación estándar σ.

Definición. Una variable aleatoria X tiene distribución normal con parámetros μ y σ², denotada X~N(μ,σ²), si su función de densidad es:

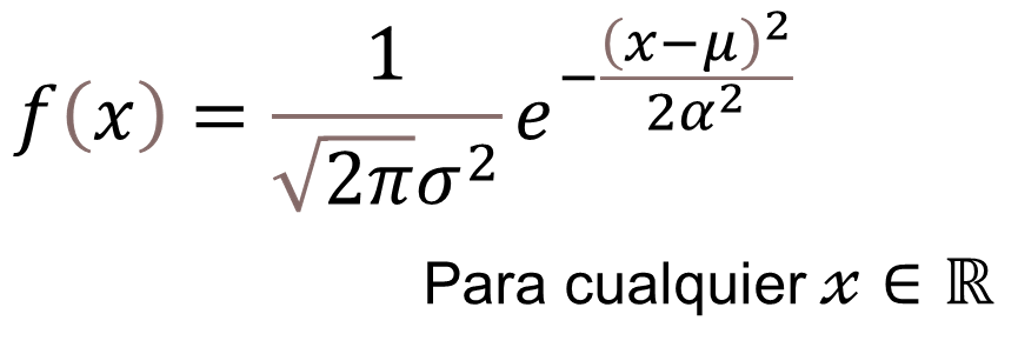
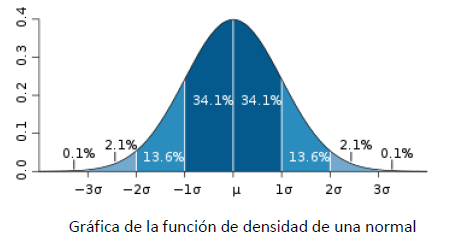
La gráfica de la curva normal es la que se presenta en la Figura 1.3.

Figura 1.3. Gráfica de la función de densidad de una normal

Propiedades de la función de densidad normal

Se demuestra que, efectivamente, la densidad normal cumple las propiedades:

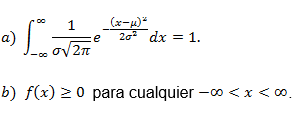
Además:

1. Tiene una única moda, que coincide con su media y su mediana.
2. La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre -∞ y ∞ es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
3. Es simétrica con respecto a su media, por lo que existe una probabilidad de 50% de observar un valor mayor que la media y 50% de observar un valor menor.
4. La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación estándar.
5. El área bajo la curva comprendida entre los valores situados aproximadamente a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de posibilidades de observar un valor comprendido en el intervalo.

Teorema: Si X es una variable aleatoria con distribución normal y con parámetros μ y σ², X~N(μ,σ²), entonces:

A diferencia de las anteriores distribuciones continuas no es fácil determinar cálculos de áreas en concreto utilizando la distribución F(x). Generalmente estos cálculos son aproximaciones y se presentan en tablas, pero éstas sólo se encuentran en la distribución normal estándar.

Da clic en el subtema 1.5.6. Distribución normal estándar para revisar el contenido.

El proceso de estandarización de una variable aleatoria consiste en un “cambio de variable”, de tal manera que la distribución obtenida con dicho cambio se comporte como normal, con media 0 y desviación estándar 1. Pero primero definamos la distribución normal estándar.

Definición. Una variable aleatoria Z tiene distribución normal estándar con parámetros μ = 0 y σ² = 1, denotada Z~N(0,1), si su función de densidad es:

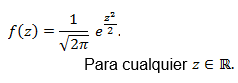
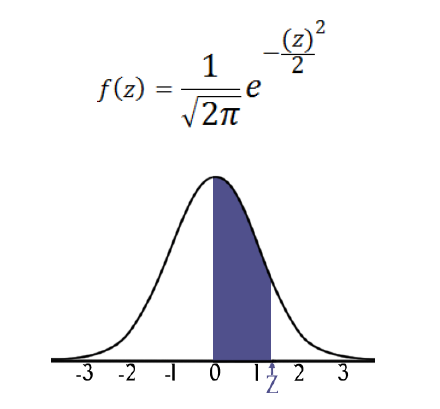
La gráfica de la densidad normal estándar es la que se presenta en la Figura 1.4:

Figura 1.4. Gráfica de densidad normal estándar

Teorema: Si Z es una variable aleatoria con distribución normal estándar Z~N(0,1), entonces:

Actualmente existe una gran variedad de tablas que aproximan con una buena precisión para valores en concreto de z la respectiva probabilidad F(z) = P(Z ≤ z).

Teorema: Si X es una variable aleatoria con distribución normal, X~N(μ,σ²) y Z = (X-μ) / σ, entonces con distribución normal estándar, Z~N(0,1).

Sea X una variable aleatoria con distribución normal, media μ y desviación estándar σ X~N(μ,σ²), considerar la variable Z = (X-μ) / σ es fácil, utilizando las propiedades de la esperanza y la varianza que esta nueva variable aleatoria Z tiene, y una media μ = 0 y desviación estándar σ = 1. Sin embargo, la demostración de la distribución de Z se puede encontrar en las lecturas referidas.

Ejemplo: Cada día más se usan las computadoras en el mundo y conforme pasa el tiempo cada casa va adquiriendo al menos una computadora. Esta computadora es usada para trabajo en casa, investigación, comunicación, finanzas personales y entretenimiento, entre otras cosas. Supón que, en promedio, el número de horas que se usa esta computadora para entretenimiento es de dos horas por día. Se asume que los tiempos de entretenimiento se distribuyen de forma normal y la desviación estándar de los tiempos corresponde a media hora. Encuentra la probabilidad de que una computadora personal sea usada entre 1.8 y 2.75 horas por día.

Sea X = la cantidad de tiempo (en horas) que una computadora es utilizada para entretenimiento. Entonces, con base en los datos X~N(2,0.5²), para calcular la probabilidad se tiene:

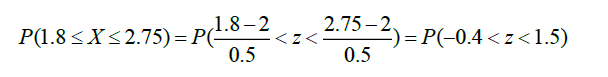
Buscando en la tabla de la distribución normal estándar para los valores z = -0.4 y z = 1.5 se tiene:

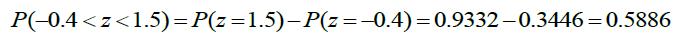
Así, la probabilidad de que una computadora personal de casa sea usada para entretenimiento entre 1.8 y 2.75 horas es de 0.5886.

Ejemplo: En una nueva compañía de construcción, la edad de los empleados contratados en los últimos cinco años tiene una distribución normal. Dentro de esta curva, 68.2% de los empleados, centrado respecto a la media, tiene entre 22.4 y 34.6 años. Encuentra la media y la desviación estándar de los datos.

En la gráfica siguiente (Figura 1.5) se muestra la distribución normal estándar. Como se puede observar 68.2% implica una extensión de 1𝜎 respecto a la media. La media es simétricamente colocada entre -1𝜎, que equivale a 22.4 años, y 1𝜎, que equivale a 34.6 años. Así, la edad media es:

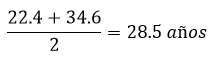
De 22.4 a 28.5 años, con una diferencia de 6.1 años, hay 1𝜎, por tanto, la desviación estándar:

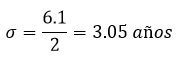
Figura 1.5. Gráfica desviación estándar

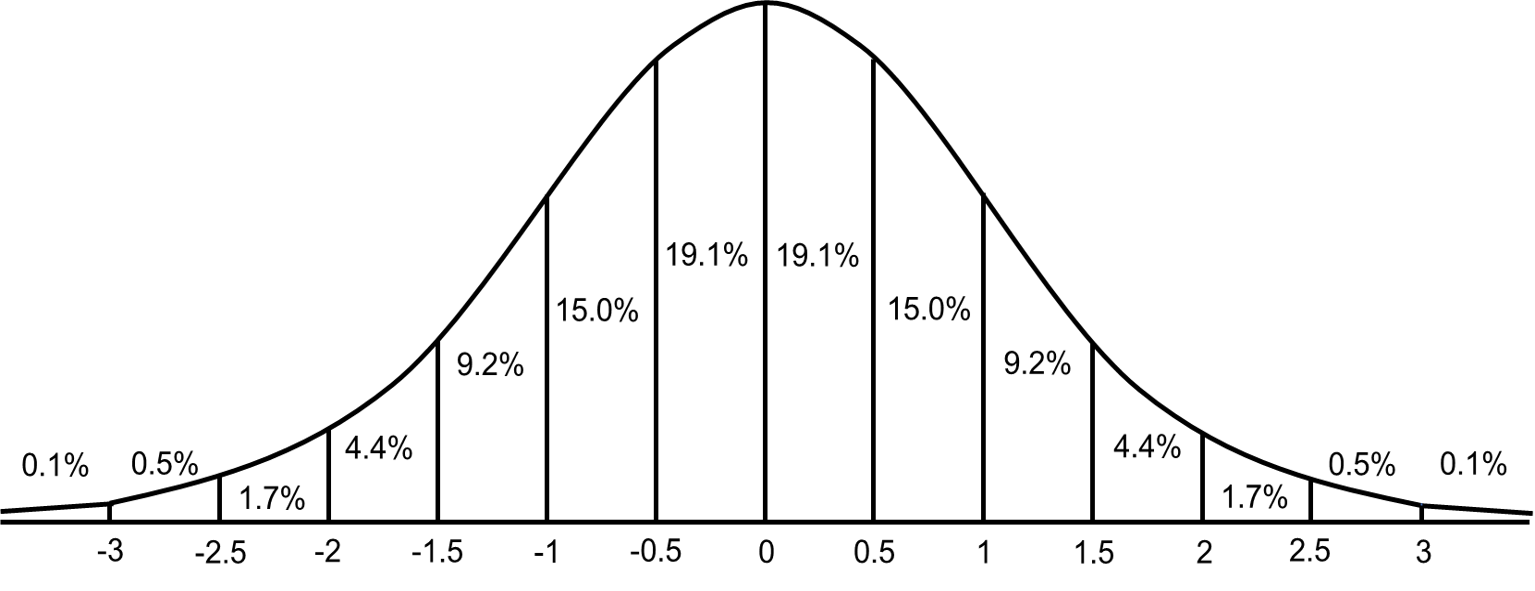
Da clic en Actividad de aprendizaje para realizar la actividad.

Da clic en el tema 1.6. Estimación para revisar el contenido.

A menudo, la función de un estadístico consiste en aproximar (estimar) el valor inaccesible o desconocido de un parámetro de la población. En tal caso, el estadístico recibe el nombre de estimador. En general, un estimador se llama insesgado si al considerarlo muchas veces, con diversas muestras de la misma población, los valores que se obtienen de él son tales que su promedio (media) tiende a ser igual que el valor del parámetro mismo que se desea estimar, a medida que se toman más y más muestras de la misma población.

La palabra insesgado significa más o menos simétrico, imparcial, centrado, equilibrado.

Existen dos formas para calcular el estimador de un parámetro: estimación puntual y estimación por intervalo.

Estimación puntual

Una estimación puntual del valor de un parámetro poblacional desconocido (como puede ser la media μ o la desviación estándar σ) es un número que se utiliza para aproximar el verdadero valor de dicho parámetro poblacional. A fin de realizar tal estimación, tomaremos una muestra de la población y calcularemos el parámetro muestral asociado (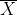 para la media, s para la desviación estándar, etc.). El valor de este parámetro muestral será la estimación puntual del parámetro poblacional.

Por ejemplo, supongamos que la compañía SuperSonic desea estimar la edad media de los compradores de equipos de alta fidelidad. Se selecciona una muestra de 100 compradores y calculan la media de esta muestra; este valor será un estimador puntual de la media de la población.

Estimación por intervalo

La estimación por intervalo requiere dar un intervalo en el cual la parte media corresponde al valor del parámetro poblacional desconocido. Este intervalo representa el porcentaje de confianza en el cual se encuentra el valor desconocido. El porcentaje de confianza varía desde el 90% hasta el 99%. No se utiliza el 100% porque no se tiene la certeza de que el valor desconocido se encuentra dentro del intervalo de confianza. Se tiene que establecer un intervalo de confianza menor al 100% por no estar completamente seguros de que el valor desconocido efectivamente se encuentra dentro de ese intervalo.

El porcentaje de confianza que más se utiliza es el de 95%, pero no es un porcentaje que forzosamente se tenga que utilizar; eso depende del que establece el intervalo de confianza. El intervalo de confianza será menor si el porcentaje de confianza aumenta. Por ejemplo, el intervalo correspondiente a 90% de confianza es mayor que el intervalo de confianza de 99%. Así, conforme el porcentaje de confianza aumenta, el intervalo disminuye. A mayor porcentaje de confianza, menor intervalo.

Es decir, a mayor nivel de confianza, el intervalo se vuelve más amplio, mientras que, a menor nivel de confianza, será un intervalo más exacto o preciso. Para calcular el intervalo de confianza, vamos a establecer los diferentes criterios:

• Si la muestra es mayor o igual a 30 datos, se debe preguntar si se conoce el valor de la desviación estándar de la población.
• Si se conoce el valor de la desviación estándar de la población, entonces, para calcular el intervalo de confianza se debe utilizar la siguiente ecuación:

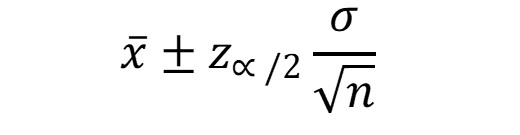
Donde:

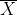= la media de la muestra
Z _∞/2 = al valor típico
σ = la desviación estándar de la población
n = al número de datos, que en este caso es superior a 30.

En caso de que se desconozca la desviación estándar de la población, se debe utilizar la desviación estándar de la muestra y emplearla en la siguiente ecuación:

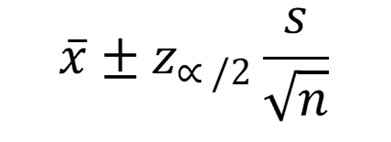
Donde:

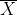= la media de la muestra
Z _∞/2 = el valor del percentil crítico
s = la desviación estándar de la muestra
n = el número de datos, que en este caso es superior a 30.

En caso de que el número de datos sea menor a 30, se debe preguntar si la distribución de la población se comporta como una distribución normal. En caso de que así sea, se debe preguntar si se conoce la desviación estándar de la población. En caso afirmativo, se debe utilizar la siguiente expresión:

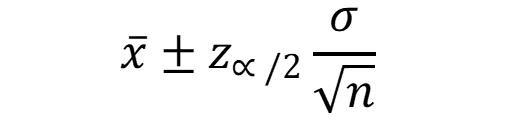
Donde:

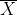= la media de la muestra
Z _∞/2 = al valor del percentil crítico
σ = la desviación estándar de la población
n = al número de datos, que en este caso es inferior a 30.

Si no se conoce el valor de la desviación estándar de la población, se debe usar la desviación estándar de la muestra para estimar la desviación estándar de la población. En este caso se debe emplear la siguiente expresión:

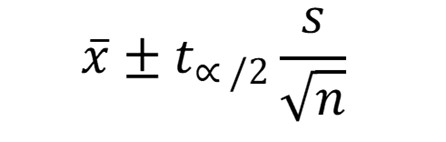
Donde:

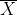= la media de la muestra
t _∞/2 = la función de distribución t-Student
s = la desviación estándar de la muestra
n = al número de datos, que en este caso es inferior a 30.

Finalmente, si la población no se comporta como una distribución normal, entonces se debe utilizar cualquiera de los dos siguientes criterios: aumentar el tamaño de la muestra o aplicar métodos estadísticos no paramétricos.

Para conocer el valor de Z _∞/2 se puede emplear Excel o la tabla de distribución normal. Si no se tiene a la mano una hoja de cálculo como Excel o la tabla de distribución normal, se puede usar la tabla de distribución t-Student con un grado de libertad infinito. Recuerda que mientras mayor sea el grado de libertad, la función de distribución t-Student se acerca más a la función de distribución normal.

Para calcular el valor de Z _∞/2 a través de Excel, debes colocarte en una celda cualquiera de la hoja de cálculo y escribir la siguiente instrucción:

=INV.NORM.ESTAND(p)

Por ejemplo, si queremos conocer el valor típico de una probabilidad del 90%, en una de las celdas se debe introducir la instrucción =INV.NORM.ESTAND(0.9). El resultado de ésta es igual a 1.96, aproximadamente. Con este valor se puede calcular el intervalo de confianza.

Ejemplo 1

Considera una muestra de 36 plantas de jitomate, cuya altura es de 2.60 m, con una desviación típica de 0.3 m y no se tiene idea de cuál pueda ser la distribución de la altura de las plantas. ¿Cuál es el intervalo de confianza de a) 95% y b) 99%?

Como la muestra es mayor a 30 datos y no se tiene idea de cuál sea la distribución de la altura de las plantas, entonces debes usar la siguiente expresión:

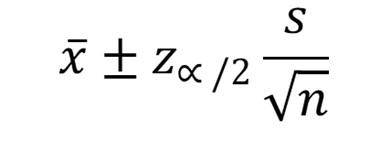
El valor de Z _∞/2 con ∞ = 5% se calcula usando la hoja de cálculo:

=INV.NORM.ESTAND(1-α/2) = INV.NORM.ESTAND(1-0.05/2) = 1.96.

Con este resultado, procedemos a sustituirlo en la ecuación anterior para conocer el intervalo de confianza:

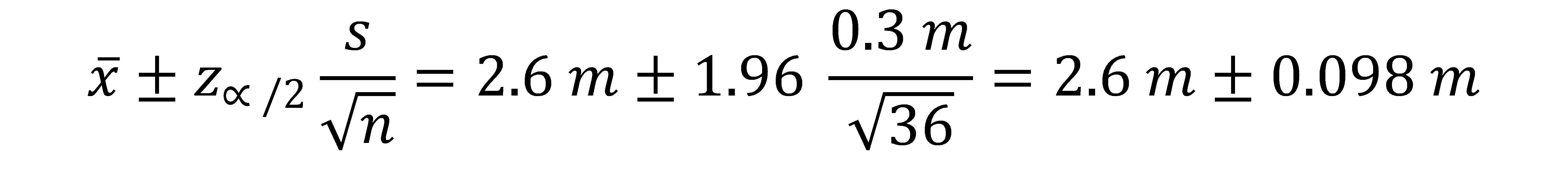
Por lo tanto, el intervalo de confianza es:

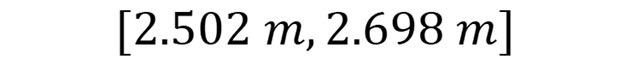
Para el caso de un porcentaje de 99% de confianza, el valor típico es igual a:

=INV.NORM.ESTAND(1-α/2) = INV.NORM.ESTAND(1-0.01/2) = 2.576.

Con este resultado, procedemos a sustituirlo en la ecuación anterior para conocer el intervalo de confianza:

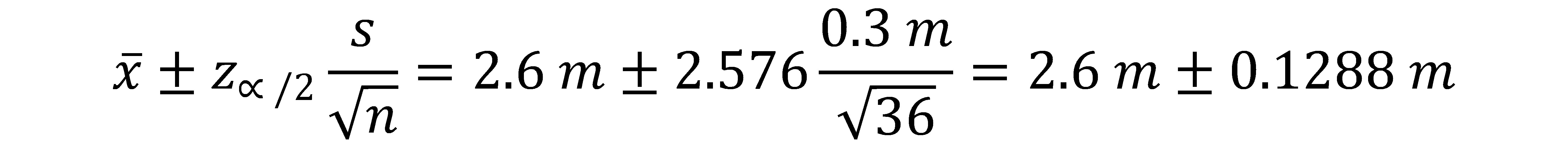
Por lo tanto, el intervalo de confianza es:

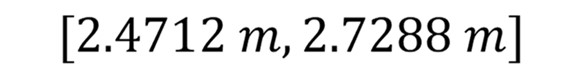
Observa que, a mayor nivel de confianza, el intervalo se vuelve más amplio. Mientras que, a menor nivel de confianza, el intervalo será más estrecho.

Ejemplo 2

Supongamos que el contenido de vitamina C en miligramos (mg), en una muestra aleatoria de 10 naranjas, es de 96.4, 86.3, 102.6, 99.0, 107.9, 84.9, 92.5, 97.2, 101.2 y 105.0. Si se sabe que la desviación estándar del contenido de vitamina C en esa variedad de naranja es de 7 mg, construir un intervalo de confianza del 95% con respecto al contenido promedio de vitamina C en esa variedad de naranja.

Sólo se debe calcular el promedio del contenido de vitamina C de los datos de la muestra, el cual es igual a 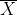= 97.3 mg. Al aplicar la ecuación que calcula el intervalo de confianza, considerando que la distribución de los valores del contenido de vitamina C se comporta como una distribución normal y que se conoce el valor de desviación estándar de la población, obtenemos:

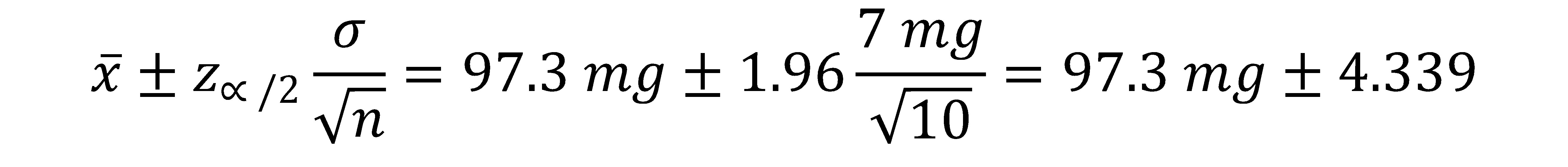
Por lo tanto, el intervalo de confianza es:

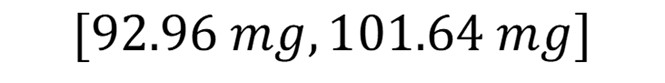
Da clic en el tema 1.7. Prueba de hipótesis para revisar el contenido.

Una prueba de hipótesis (también llamada ensayo de hipótesis, contraste de hipótesis o prueba de significación) es una parte fundamental de la inferencia estadística.

Una prueba de hipótesis es un procedimiento estadístico simple cuya finalidad es corroborar o desmentir alguna afirmación que se hace en relación con un parámetro poblacional.

Para hacer esto, se toma una muestra aleatoria de la población y se calcula el valor de un estadístico de prueba, el cual debe obedecer ciertas leyes estadísticas comprobadas. Según como resulte o se comporte el estadístico de prueba, se podrá aceptar o rechazar alguna hipótesis previamente establecida. Al emitir la decisión final de rechazar o aceptar la hipótesis original, se corre el riesgo de equivocarse y darle un valor significativo erróneamente a algo que solo ocurrió de manera fortuita. Esto es inevitable, porque el azar siempre está presente.

Al realizar una prueba de hipótesis podemos cometer dos tipos de error, llamados universalmente error tipo I y error tipo II.

El error de tipo I consiste en rechazar una hipótesis que es cierta, pero que debería haberse aceptado.

El error de tipo II consiste en aceptar como válida una hipótesis que es falsa, pero que debería haberse rechazado.

La hipótesis nula es una suposición inicial que sirve para echar a andar el procedimiento de una prueba o verificación de una hipótesis estadística relativa a algún parámetro de una población. Por lo general, se usa el símbolo H₀ para denotar la hipótesis nula.

Es importante señalar que una hipótesis nula siempre debe estar expresada mediante una igualdad (=) o cuando mucho un signo de menor o igual (≤) o de mayor o igual (≥). No se puede establecer una hipótesis nula que involucre un solo signo de desigualdad, menor que (<) o bien mayor que (>). La hipótesis nula debe ser en principio inocua o inofensiva.

La hipótesis alternativa establece lo contrario de la hipótesis nula. Si ésta es rechazada, entonces será la hipótesis alternativa la que se tome tentativamente como válida, y viceversa. Se dice tentativamente porque de ninguna manera se acepta de manera tajante y concluyente, pues quizá alguna prueba futura, realizada con mayor precisión, podría ponerla en tela de juicio. Una hipótesis alternativa se denota por el símbolo H_a o también por el símbolo H₁.

El nivel de significación de una prueba es la probabilidad máxima de cometer un error tipo I y dicha probabilidad se suele denotar universalmente por la letra α. Lo más usual es que al principio se establezca cuál es el valor de α que se desea aplicar en la prueba. Resulta común tomar valores de α = 0.05 o bien α = 0.01.

A la probabilidad máxima de cometer un error de tipo II se denota por la letra β. Aunque no tiene un nombre especial, al número 1 - β se le llama potencia de la prueba. Si la hipótesis alternativa es vaga, en el sentido de que involucra un signo < o >, entonces no se puede cuantificar el valor de β. Para poder calcular un valor numérico de β, se necesita que la hipótesis alternativa sea específica, esto es, que involucre el signo =.

El estadístico de prueba es una magnitud calculada mediante una muestra aleatoria y que involucra algún estadístico o combinaciones de estadísticos y cuyo valor se usará finalmente para contrastar con algún valor estadístico tabulado, y entonces decidir si procede o no el rechazo de la hipótesis nula.

Por eso, una prueba de hipótesis se llama también contraste de hipótesis porque, a fin de cuentas, el momento de decidir si se rechaza o no la hipótesis nula ocurre al contrastar el valor numérico de un estadístico de prueba con otro valor numérico, usualmente tabulado, que rige el comportamiento hipotético de la población de donde se extrajo la muestra, de acuerdo con la distribución supuesta.

Ésta es una ley fundamental en estadística que establece que si dos supuestos de distribución son correctos, entonces los estadísticos observados en diferentes muestras tienden como límite a los parámetros teóricos correspondientes cuando el tamaño de muestra tiende a infinito; en particular las frecuencias relativas observadas tienden a las probabilidades teóricas como límite.

La regla de decisión es una especificación clara de cuándo se rechazará la hipótesis nula y cuándo no se rechazará. La regla de decisión siempre está relacionada con el nivel de significación α de la prueba, en el sentido de que si se conoce α de antemano, entonces la regla de decisión se deduce de manera única, y recíprocamente: si sólo se dispone de una regla de decisión al principio, entonces, no se debe establecer ningún valor de α, ya que éste quedará determinado en forma automática, de acuerdo con la regla de decisión elegida.

No se deben especificar ambas cosas de antemano, el valor de α y la regla de decisión, ya que podrían ser contradictorios. En la mayoría de los casos, se acostumbra especificar el valor de α al principio, y entonces la regla de decisión se deduce o se infiere, de acuerdo con el modelo. Pero no hay nada malo en hacerlo al revés.

Procedimiento para una prueba de hipótesis en general

1. Se emite una hipótesis nula (H₀) relativa a algún parámetro de la población. La hipótesis debe involucrar alguno de los signos = , ≥ o ≤, pero no puede involucrar ninguno de los signos ≠, < y >, los cuales se reservan para la hipótesis alternativa. Al mismo tiempo se especifica la hipótesis alternativa H_a, lo cual establece lo contrario de la hipótesis nula.
2. Se especifica un nivel de significación σ a usar. Lo convencional es emplear los niveles de 5% (σ = 0.05) o del 1% (σ = 0.01), pero ello no es obligatorio.
3. Se extrae de la población una muestra aleatoria de tamaño n y se calcula el estadístico de prueba apropiado.
4. Se compara el valor numérico obtenido para el estadístico de prueba con el valor numérico correspondiente del modelo teórico que se va a seguir, usualmente empleando las tablas de percentiles o de valores críticos de alguna distribución estadística teórica.
5. De acuerdo con el contraste de valores numérico del paso anterior, se decide si se rechaza la hipótesis nula o no se rechaza, bajo el entendido de que, si no se rechaza, entonces significa que se acepta sólo de manera tentativa o provisional, a reserva de efectuar pruebas ulteriores que corroboren o desmientan esta decisión.

Como aplicación de la prueba de hipótesis, se tienen los siguientes ejemplos:

Ejemplo 1

Los paquetes de café Bemoka, de Colombia, de medio kilogramo dicen “contenido neto 500 g”. Se eligieron al azar 50 paquetes y se pesaron con una balanza analítica, tras lo cual se registraron los siguientes datos muestrales:

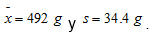
A primera vista, parece que el peso neto promedio de los paquetes fuera tal vez menor que el anunciado. Efectúa una prueba de nivel de σ = 0.05 para probar la hipótesis.

La hipótesis nula es igual a H₀:μ = 500g contra la hipótesis alternativa:

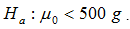
F^-1 = (0.05) = -1.645 y el valor del estadístico de prueba es:

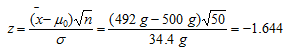
Aunque es un número muy parecido al del valor crítico, queda a la derecha de éste, es decir, queda en la zona de aceptación. Por tanto, no es posible rechazar la hipótesis nula, y la prueba muestra que no hay razones para suponer que el contenido neto medio de los paquetes es menor que el anunciado.

Ejemplo 2

El departamento de seguridad de una fábrica desea saber si el tiempo promedio real que requiere el velador para realizar su ronda nocturna es de 30 minutos. Se tomó una muestra al azar de 32 rondas y el velador promedió 30.8 minutos con una desviación estándar de 1.8 minutos. Realiza una prueba de hipótesis con σ = 0.01, que permita averiguar si hay evidencia suficiente para rechazar la hipótesis nula en favor de la hipótesis alternativa.

La hipótesis nula es igual a H₀:μ = 30 min, contra la hipótesis alternativa:

H₀:μ ≠ 30 min Se trata de un ensayo bilateral (dos colas). Los valores críticos son aquéllos con áreas respectivas de 0.005 en sendas esquinas bajo la curva, es decir, ±2.576. El estadístico de prueba es:

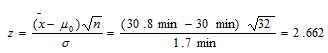
Este valor cae en la zona de rechazo, porque es mayor que 2.576. Por consiguiente, se rechaza la hipótesis de que el tiempo promedio real que hace el velador en sus rondas es de 30 minutos, por lo que concluimos que es muy probable que el velador haga un tiempo diferente de 30 minutos. Por lo que hay un 99% de que el tiempo que tarda un velador sea diferente de 30 minutos. Desde luego existe un 1% de probabilidad de que esa diferencia en el tiempo sea por obra del azar.

Ejemplo 3

En cierto país se estableció que hace 20 años el promedio de vida de una persona era de 71.4 años. Recientemente se tomó una muestra aleatoria de 100 muertes y se obtuvo que la media muestral fue de 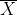= 73.8 años, con una desviación estándar de 9.8 años. ¿Son significativos estos datos para argumentar que actualmente la gente vive, en promedio, más que hace 20 años?

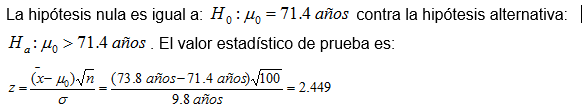
El valor de la probabilidad de que sea mayor que 71.4 años el promedio de vida es igual a F(2.449) = 1-0.992857 = 0.007163 < 0.01. Por lo tanto, se rechaza la hipótesis nula y se concluye que los resultados de la muestra son altamente significativos para argumentar que en la actualidad las personas viven en promedio más que hace 20 años.

Da clic en la Evidencia de aprendizaje para realizar la actividad.

Da clic en Fuentes de consulta para revisar las fuentes.

Básica

• Ascencio, I., Carballo, R., Fernández, M. J. y García, J. M. (2011). Problemas de Estadística Aplicadas a la Educación. Madrid, España: Síntesis.
• Braun, E. (2007). Caos, Fractales y Cosas Raras. México, D. F.: Fondo de Cultura Económica.
• Clifford, R. y Taylor, R. A. (2008). Bioestadística. México, D. F.: Pearson Prentice Hall.
• Galán, A., García, J. L., Gil, J. A. y Pérez, R. (2009). Estadística Aplicada a la Educación. Madrid, España: Pearson Prentice Hall.
• Ruiz, E. (2007). Probabilidad y estadística. México: McGraw-Hill.
• Wisniewski, P. M. y Velasco Sotomayor, G. (2001). Problemario de probabilidad. México, D.F., México: Thomson.

Complementaria

• Anderson, D. y Sweeney, D.J. (2008). Estadística para administración y economía. Cengage Learning Latin America.
• Devore, J. L. (2005). Probabilidad y estadística para ingeniería y ciencias. México: Thomson.
• Evans, M. J. (2005). Probabilidad y estadística. Reverte.
• Gamiz-Casarrubias, B. (2003). Probabilidad y estadística con prácticas en Excel. México: Just in time Press.
• Hayslett, H. T. Jr. (1987). Estadística simplificada. México: Grupo editorial Sayrols.
• Johnson, R. y Kuby, P. (2006). Estadística elemental. México: Thomson Paraninfo.
• Lincoln L., Ch. (2000). Introducción a la estadística. México: Compañía Editorial Continental.