Para poder construir modelos, primero necesitamos entender qué es un modelo matemático. A grandes rasgos, es la representación de un fenómeno real basada en relaciones matemáticas. Todas las fórmulas, gráficas o tablas que describen de alguna manera el comportamiento de un sistema real, son modelos matemáticos.

Debido a la complejidad de los fenómenos de la naturaleza, casi siempre, al construir un modelo matemático, se tienen que hacer simplificaciones que hacen que esta imagen matemática sea una aproximación a la realidad que se trata de reproducir. Por lo mismo, hay que distinguir claramente entre el modelo como representación y la realidad misma.

Este carácter aproximativo de los modelos, más que un defecto, resulta ser una de sus ventajas. Uno pensaría que lo más deseable sería una representación matemática idéntica al fenómeno. Esto generalmente es imposible, además de que sería poco útil, ya que el modelo resultaría muy difícil de analizar. Lo que se debe buscar es que el modelo sea simple y que reproduzca fielmente las características importantes del fenómeno. Así, éste es incluido en un marco teórico que es más fácil de analizar.

Es recomendable empezar desarrollando un modelo relativamente simple y poco a poco irlo mejorando. Esta es una buena estrategia de modelación, ya que al ir introduciendo cada factor podemos observar su efecto. Así, el mismo proceso de la construcción del modelo favorece el aprobar o rechazar hipótesis que serían muy difíciles de comprobar de manera experimental.

Para un fenómeno particular, podemos construir una infinidad de modelos matemáticos. Unos enfocados a a determinadas características del fenómeno, otros a las que restan; unos más complejos y otros más simples. Así, los modelos matemáticos no se pueden clasificar como correctos o incorrectos. En su lugar, se habla de si un modelo es apropiado o no a cierta situación. Para esto nos basamos en las limitaciones del modelo que se generan de su propio diseño.

La ecuación de caída libre, por ejemplo, nos ayuda a entender la relación de distancia y tiempo de un objeto en caída. Sin embargo, debemos conocer sus limitaciones para poderla usar en predicciones. De esta manera, la caída de una hoja de papel no puede representarse con este modelo, ya que la resistencia al factor aire es muy grande en este caso, la cual no está considerada en la ecuación. Por lo tanto, podemos decir que este modelo es aplicable en situaciones donde la resistencia del aire sea despreciable.

Un peligro de los modelos matemáticos es que resultan tan idealizados y sin bases reales que se aproximan muy levemente a su contraparte real. Aquí nos interesa presentar las ideas matemáticas y los modelos que están basados directamente en observaciones del mundo real, tratando siempre de mantener esta conexión entre el modelo y el fenómeno. Debemos aclarar, sin embargo, que la simplificación es esencial en la modelación y que no debe confundirse con la sobreidealización del comportamiento del fenómeno.

Existen modelos con un comportamiento exponencial. Es un error pensar que estos modelos no representan la realidad de manera razonable. Por ejemplo, en biología un modelo exponencial para poblaciones es incorrecto, ya que las poblaciones no pueden crecer hacia el infinito, como lo hace el modelo. Hay que entender que esta suposición de crecimiento exponencial es sólo una simplificación que hace al modelo más manejable. Además, los modelos exponenciales son aplicables a poblaciones que no tengan limitantes de crecimiento, como células de un laboratorio o poblaciones humanas sin restricciones severas de alimento. El modelo exponencial es entonces adecuado en un buen rango de crecimiento de estas poblaciones.

Otra de las características de un modelo matemático es que es intrínsecamente aproximado y, por lo tanto, sus resultados deben de interpretarse de acuerdo con esto. Por ejemplo, los modelos de poblaciones dan, por lo general, resultados decimales. Esto no quiere decir que los modelos sean incorrectos, sino que sólo son aproximaciones a la realidad y que, por lo tanto, se debe considerar solamente la parte entera de los resultados.

Da clic en el tema 3.2. Clasificación de los modelos matemáticos para revisar el contenido.

La actividad científica es inconcebible sin el desarrollo de modelos matemáticos que permitan sintetizar e incrementar el conocimiento existente sobre un sistema. La investigación agrícola y, en especial, la ciencia y arte de la horticultura no son la excepción. Los modelos matemáticos de hortalizas permiten probar hipótesis científicas y, además, tienen aplicación potencial tanto en educación como en la práctica de la horticultura. Por ejemplo, los modelos permiten evaluar estrategias del manejo posible de un invernadero sin necesidad de llevar a cabo experimentos costosos.

En general existen tres tipos de modelos matemáticos:

Los modelos empíricos, que son descripciones directas de datos y proporcionan relaciones observables entre las variables de un sistema o fenómeno, sin proporcionar alguna explicación de los mecanismos subyacentes. Estos modelos son un poderoso medio para describir y resumir datos. Ejemplos de ellos son los modelos de regresión simple y regresión múltiple, redes neuronales, modelos difusos o modelos neurodifusos.

Los modelos teleonómicos, que son aplicables a comportamientos dirigidos por metas y se formulan explícitamente en términos de objetivos.

Los modelos explicativos o mecanicistas, que, por lo general, son modelos determinísticos. Normalmente, un modelo mecanicista es definido mediante un conjunto o sistema de ecuaciones diferenciales ordinarias no-lineales, las cuales describen el comportamiento de las variables de estado del sistema, es decir, aquellas variables que representan las propiedades relevantes o atributos del sistema considerado. El desarrollo de un modelo matemático mecanicista requiere de suficiente comprensión de los procesos biológicos, fisiológicos, químicos y físicos de un sistema biológico. El uso de un modelo mecanicista demanda análisis, calibración y validación apropiados.

Da clic en el tema 3.3. Funciones matemáticas y modelos matemáticos para revisar el contenido.

3.3.1. Función lineal

Entre las relaciones empíricas, la curva más simple que se podría obtener al graficar una serie de datos experimentales es la línea recta y corresponde a las llamadas relaciones lineales.

Una relación de este tipo es una línea recta que representa el comportamiento de un fenómeno. Indica que hay una relación de proporcionalidad entre las variables en cuestión y que, por lo tanto, existe una constante de proporcionalidad que, en este caso, es la pendiente de la recta.

La ecuación general que representa a una relación lineal es la ecuación de la recta de la forma:

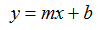
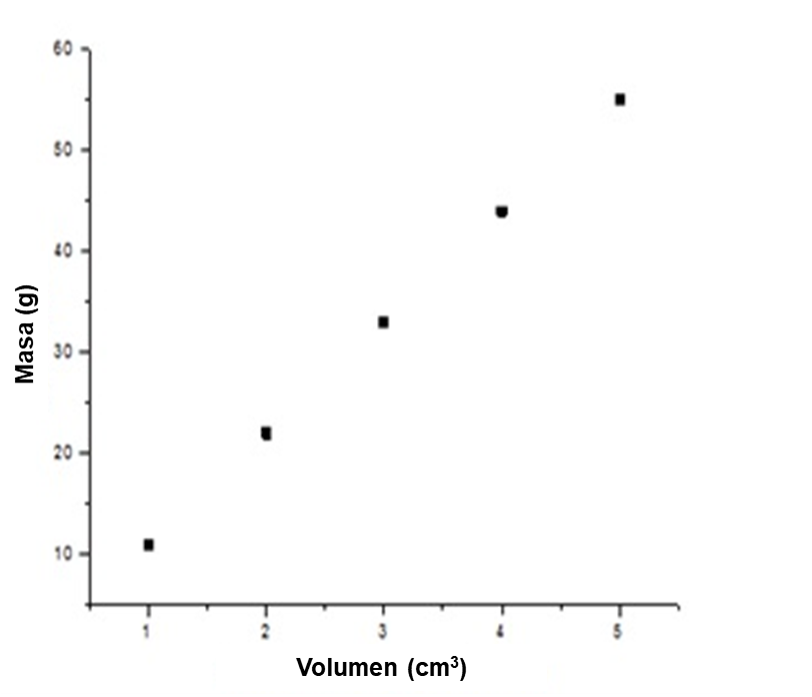
Donde x representa la variable independiente y y a la variable dependiente. Si P1 y P2 son puntos de la recta con coordenadas P₁ = (X₁,Y₁) y P₂ = (X₂,Y₂), la llamada pendiente de la recta se calcula como:

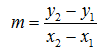
Y la ordenada al origen se calcula como:

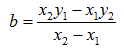
Supongamos que se tienen diferentes muestras de hierro, con las cuales se efectuaron mediciones de las masas y los volúmenes respectivos. Los datos obtenidos se muestran en la Tabla 3.1.

Tabla 3.1. Datos de la masa en función del volumen

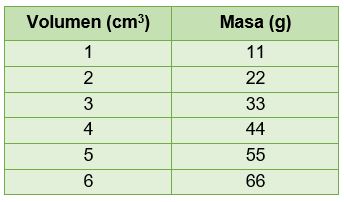
Los datos de la tabla anterior se grafican en la Figura 3.1. Utilizando dos datos de la recta y sustituyéndolos en las fórmulas para calcular la pendiente y la ordenada al origen, se tiene:

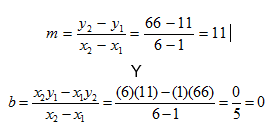
Figura 3.1. Masa del hierro en función del volumen

Como se puede observar, el valor de la ordenada al origen es igual a cero. Esto indica que la recta pasa por el origen, y la masa sobre el volumen es igual a 11 gramos por cada centímetro cúbico. Por lo que la pendiente de la recta representa la densidad del hierro.

Da clic en el tema 3.3.2. Función cuadrática para revisar el contenido.

Una relación cuadrática es una línea parabólica que representa el comportamiento de un fenómeno. Este tipo de relación no implica que hay una relación de proporcionalidad entre las variables en cuestión y que, por lo tanto, no existe una constante de proporcionalidad que, en este caso, es la pendiente de la recta.

La ecuación general que representa a una relación cuadrática es una ecuación de segundo grado de la forma:

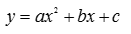
Donde a, b, y c son constantes.

Este tipo de ecuación representa una parábola. Si el valor de a es positivo, la parábola abrirá hacia arriba, pero abrirá hacia abajo en caso contrario. Si los valores de a y de b tienen el mismo signo, el vértice de la parábola se encontrará a la izquierda del eje de las ordenadas, y si sus signos son diferentes, se encontrará a la derecha.

Finalmente, si el valor de c es positivo, el cruce de la parábola con el eje de las ordenadas será por arriba del origen y si el valor de c es negativo, el cruce será por debajo. Esto es cierto independientemente del valor que asuma el valor de a y b.

Como son tres las constantes que se encuentran en la ecuación de la parábola, mínimo se necesitan tres datos para encontrar sus valores. Si quisiéramos conocer la ecuación que se relaciona con los datos de la Tabla 3.2, al menos se necesitan tres datos para conocerlos.

Tabla 3.2. Valor de y en función de x

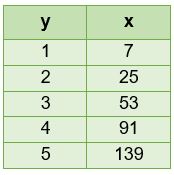
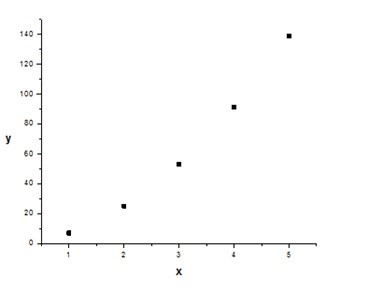
La siguiente Figura 3.2 muestra la gráfica de los datos de la tabla anterior.

Figura 3.2. Valor de y en función de x

Si se quisiera conocer el valor de las constantes a, b y c, es necesario sustituir en la ecuación de la parábola tres valores de los que se encuentran en la tabla. Por ejemplo, se pueden utilizar el primero, tercero y quinto dato para sustituirlos en la ecuación mencionada:

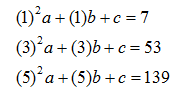
Resolviendo este sistema de ecuaciones, se concluye que a = 5, b = 3 y c = -1. Como a y b son positivos, el vértice de la parábola se encuentra a la izquierda del eje de las ordenadas y el cruce de la parábola con el eje de las ordenadas se encuentra por debajo del origen.

Da clic en el subtema 3.3.3. Función potencial para revisar el contenido.

Serán llamadas funciones potenciales todas aquellas funciones que puedan ser representadas por ecuaciones de la forma:

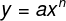
Donde y y x son variables y a y n son constantes.

De acuerdo con el exponente n , se pueden distinguir dos tipos de curvas: parabólicas si n es positiva e hiperbólicas si n es negativa.

Para conocer el valor de la a y de la n, se utiliza una técnica llamada cambio de variable, donde a cada uno de los valores de la tabla que relaciona a y y x se le aplica la función logaritmo para linealizar la curva.

Por ejemplo, supón que se tienen los datos de la distancia y la intensidad luminosa (Tabla 3.3):

Tabla 3.3. Intensidad luminosa en función de la distancia

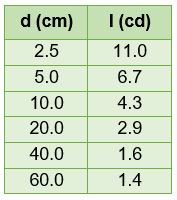
La Figura 3.3 muestra la gráfica de los valores expresados en la tabla.

Figura 3.3. Intensidad luminosa en función de la distancia

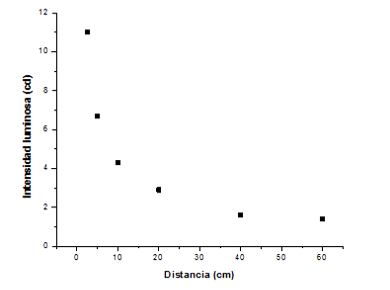
Vemos que la gráfica es de tipo hiperbólica, por lo que se debe hacer un cambio de variable para conocer el valor de a y n. El cambio de variable consiste en aplicar la función logaritmo en base 10 para linealizar la curva. El valor de la pendiente y de la ordenada al origen corresponde al valor de n y de a, respectivamente.

La Tabla 3.4 muestra los valores del logaritmo de la intensidad luminosa y de la distancia.

Tabla 3.4. Logaritmo de la intensidad luminosa en función del logaritmo de la distancia

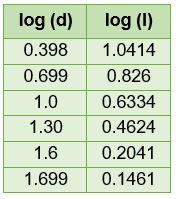
La Figura 3.4 muestra la gráfica del logaritmo de la intensidad luminosa en función del logaritmo de las distancias.

Figura 3.4. Logaritmo de la intensidad luminosa en función del logaritmo de la distancia

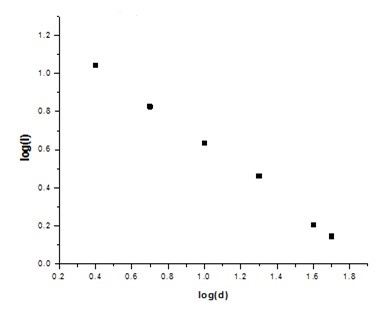
Vemos en la gráfica que los puntos conforman una línea recta, cuya pendiente y ordenada al origen se pueden calcular con las ecuaciones:

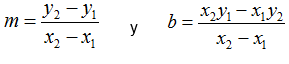
Tomando dos puntos de la recta, se tiene:

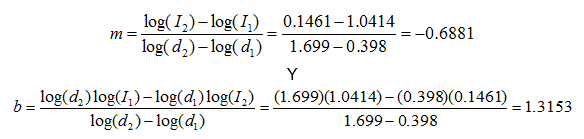
Por lo que la ecuación de la recta es igual a:

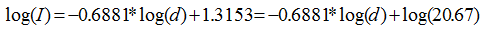
Aplicando las reglas de los logaritmos, se tiene:

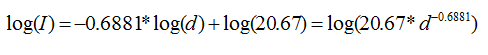
Aplicando la función inversa del logaritmo a la ecuación anterior, se llega a:

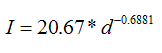
En consecuencia, al aplicar la función logaritmo a la Intensidad luminosa y a la distancia, se obtiene una línea recta cuya pendiente y ordenada al origen es igual al exponente de la distancia y al coeficiente, respectivamente.

Da clic en el subtema 3.3.4. Función exponencial para revisar el contenido.

Supongamos que el valor de un automóvil nuevo es de $ 200 000.00 y que éste pierde el 20% de su valor cada año. Queremos predecir su valor después de seis años. Para el primer año se tiene que el valor original del automóvil perdió $ 40 000.00, así que el valor del auto al primer año es de $ 160 000.00. En el segundo año volverá a perder el 20% del valor que tenía el automóvil al primer año, que sería de $ 32 000.00. De esta forma, el valor del automóvil al segundo año sería de $ 128 000.00, y así sucesivamente.

Se puede construir una tabla (Tabla 3.5) en donde se muestren los valores del automóvil para cada año:

Tabla 3.5. Precio del automóvil en función de tiempo

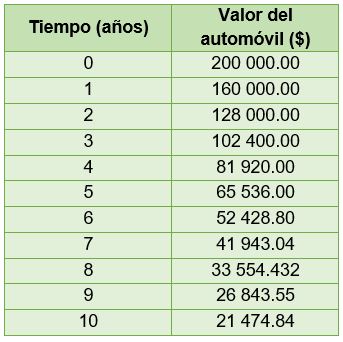
Notamos en la tabla que a los tres años el valor del automóvil se reduce casi a la mitad. Por ello decimos que el valor medio del automóvil es de tres años. De igual forma, se observa que a pesar de que siempre es el mismo porcentaje de depreciación, conforme pasa el tiempo es menor la diferencia de precios entre un año y otro.

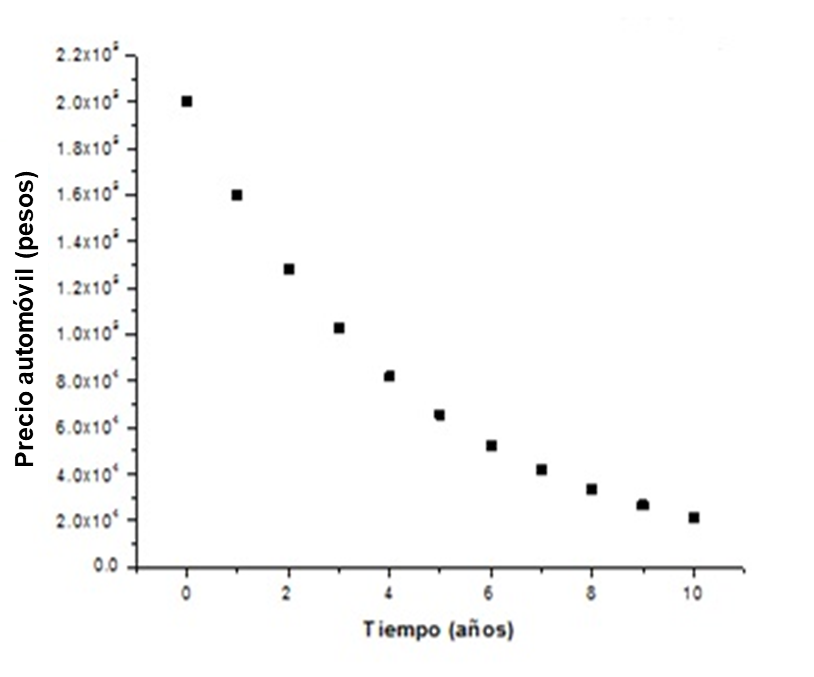
Es decir, mientras más tiempo transcurra, más lenta será la depreciación del automóvil. Una forma muy útil de mostrar los datos es por medio de una gráfica. Ésta nos ayudará a representar los resultados de una manera global. Al construir la gráfica (Figura 3.5) de los valores anteriores, extendiéndolos hasta el décimo año, obtendremos:

Figura 3.5. Precio del automóvil en función del tiempo

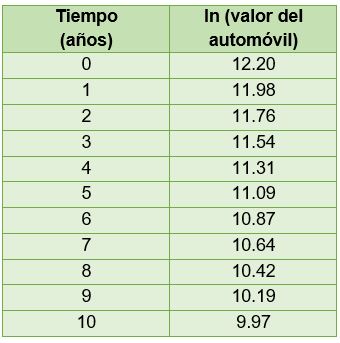
Para poder convertir en una línea recta la curva de la gráfica anterior, apliquemos a cada uno de los valores del automóvil la función logaritmo natural. La Tabla 3.6 muestra el logaritmo natural del tiempo y su respectivo valor del automóvil.

Tabla 3.6. Logaritmo del precio del automóvil en función del tiempo

La Figura 3.6 muestra la gráfica del logaritmo natural del precio del automóvil en función del tiempo.

Figura 3.6. Logaritmo natural del precio del automóvil en función del tiempo

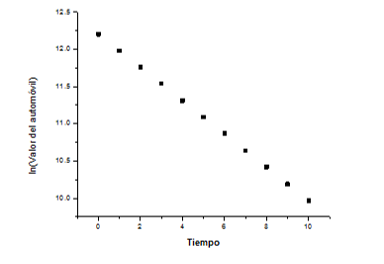
Vemos que es una línea recta, cuya ecuación se puede deducir de la siguiente manera:

Tomemos dos puntos de la recta, por ejemplo, el primero y el noveno, y sustituyámoslos en la siguiente ecuación:

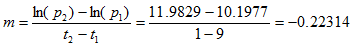
Esta proporción debe ser igual a la proporción que existe entre uno de los puntos escogidos y otro cualquiera de la recta, es decir:

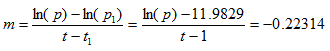
Despejando el logaritmo natural expresado en la ecuación anterior, tenemos:

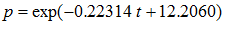
Utilizando la regla de los exponentes, se tiene:

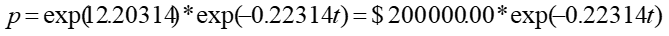
En consecuencia, la expresión que calcula el precio del automóvil en función del tiempo depende de una función exponencial. Así, $ 200 000.00 expresa el valor del automóvil en el momento de la compra y -0.22314 es la constante de la exponencial por la cual se va depreciando en automóvil.

Para conocer el tiempo por el cual el valor del automóvil es igual a la mitad, sustituyamos en el precio la mitad de su valor original, es decir:

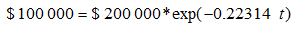
Despejando se tiene:

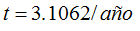
Vemos que aproximadamente en tres años se deprecia el valor del automóvil a la mitad.

Da clic en el subtema 3.3.5. Método de mínimos cuadrados para revisar el contenido.

Supongamos que en cierto experimento aleatorio tratamos de manera simultánea con dos cantidades, una variable ordinaria X y una variable aleatoria Y, cuya medida depende de X, y efectuamos el experimento de tal manera que seleccionamos primero n valores de X, y luego, para cada X, obtenemos un valor observado de Y. Entonces tenemos una pareja de n muestras de X y Y.

Con el fin de ver qué relación tienen ambas variables, podemos graficar cada par de parejas en el plano cartesiano. En algunos casos podemos ver que los n puntos se encuentran muy cercanos a una recta, y podemos ajustarla a “ojo de buen cubero”. A esta recta se le llama recta de regresión de los valores de la muestra de Y con base en los valores de la muestra de X.

Ésta se puede utilizar para predecir valores de Y para alguna X dada que nos interese, de tal manera que obtengamos alguna idea de la relación que existe entre estas dos variables.

Cuando ajustamos, existe la posibilidad de que diferentes personas puedan ajustar, sin los cálculos adecuados, rectas completamente diferentes. Por lo tanto, debemos tener un método matemático para ajustar rectas que den un resultado único que sólo depende de los puntos y no de la persona.

Un procedimiento de este tipo, que es muy utilizado, es el método de mínimos cuadrados, desarrollado por Gauss. En nuestra situación puede formularse de la siguiente manera:

La recta debe ajustarse a los puntos dados de manera que la suma de los cuadrados de las distancias de estos puntos hasta la recta sea mínima, en donde la distancia se mide en dirección vertical.

Es evidente que las distancias intervienen en el método. El usar cuadrados de distancias, en lugar de valores absolutos, resulta práctico desde el punto de vista del cálculo y de la teoría. Esto hace preferible este método, en comparación con otros métodos que pueden usarse para el mismo fin. El uso de la distancia vertical se justifica por el hecho de que X es una variable independiente, cuyos valores se seleccionan al principio del experimento y que deseamos estimar valores de Y que corresponden a valores dados de X.

La fórmula que calcula el valor de la pendiente y de la ordenada al origen de una serie de datos que se conforman aproximadamente como una recta está dada por las fórmulas de mínimos cuadrados:

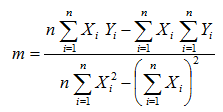
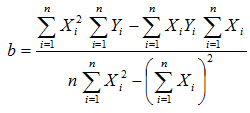
Donde m es la pendiente de la recta y b es la ordenada al origen.

La recta se llama recta de regresión de los valores de Y de la muestra con base en los valores de X.

Da clic en Actividad de aprendizaje para realizar la actividad.

Da clic en el tema 3.4. Fases para la creación de un modelo matemático para revisar el contenido.

La construcción de un modelo matemático sigue una serie de fases que no necesariamente son una regla, pero que nos permiten tener una guía sobre el proceso de modelación (De Torres, 2015, p. 24):

En primer lugar, es importante tener claro el propósito de lo que queremos modelar y por qué; luego es necesario identificar los componentes del modelo y sus relaciones, que después se convertirán en ecuaciones; una vez armado el modelo, normalmente se compone de parámetros, es decir, constantes indeterminadas que deberemos remplazar por valores numéricos.

La construcción del modelo suele incluir datos, los cuales se obtienen de experimentos de laboratorio y de observaciones de campo, o bien de resultados de otras investigaciones. Esta información nos permite dar a los parámetros los valores numéricos adecuados. A esta inclusión de la información de la realidad se le conoce como calibración del modelo.

El siguiente paso es la validación, que consta de la comparación de los valores de salida del modelo con valores empíricos de dichas variables, lo que se denomina verificabilidad. El propósito de esta comparación es evaluar el error cometido por el modelo y determinar si podemos tolerarlo. Aquí es necesario el conocimiento previo que el investigador tiene del sistema para contrastar los resultados teóricos con los empíricos y de esta forma validar o no el modelo.

Posteriormente, viene la fase del análisis de sensibilidad, que consiste en preguntarse qué tanto se podrían modificar los resultados del modelo si los valores de las variables o los parámetros cambiaran un poco. Este paso es crucial, ya que si el modelo se dispara a valores totalmente distintos cuando se producen pequeñas modificaciones en los valores numéricos, no será un modelo confiable, puesto que pequeños errores en la medición podrían generar resultados muy diferentes.

Una vez que sabemos que el modelo funciona en esta realidad, podemos ponerlo a funcionar en otros escenarios hipotéticos. Esta fase se conoce como simulación.

Finalmente, para terminar el estudio de esta asignatura, revisaremos algunos ejemplos de modelos matemáticos aplicados a la agricultura. No se mencionan todos, dado que el número de éstos depende de las necesidades que van surgiendo en las diferentes dimensiones de la seguridad alimentaria.

Modelos matemáticos aplicados al crecimiento de las plantas

Los modelos matemáticos aplicados al crecimiento de las plantas permiten estimar o predecir su comportamiento temporal en diferentes condiciones. La mayor parte de los modelos matemáticos se pueden clasificar en modelos lineales y no lineales. A continuación se muestran cada uno de los modelos que constituyen los lineales y los no lineales:

Modelos lineales

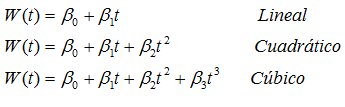
Modelos no lineales

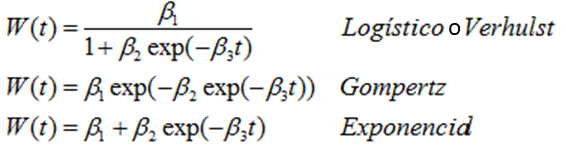
Donde:

W(t) = la variable que representa el crecimiento o desarrollo.
β_i= los parámetros de los modelos i = 0, 1, 2 y 3.
t= el tiempo.

Da clic en el tema 3.5. Modelos matemáticos aplicados a la seguridad alimentaria para revisar el contenido.

3.5.1. Modelo de crecimiento del jitomate

Uno de los modelos de crecimiento para el jitomate es el correspondiente al modelo de Gompertz. A continuación en la Tabla 3.7 se muestran las diferentes alturas de la planta del jitomate para diferentes tiempos:

Tabla 3.7. Datos de la altura de la planta del jitomate en función de la edad

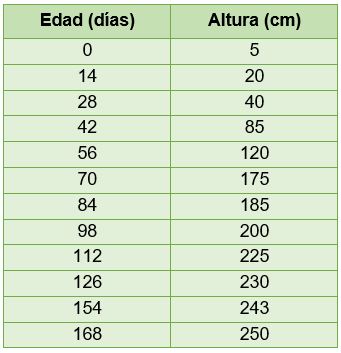
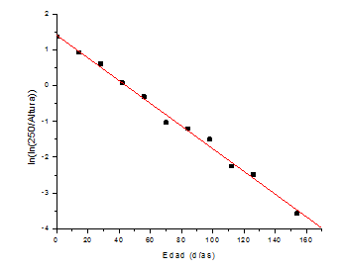
La Figura 3.7 muestra la gráfica de los datos representados en la tabla anterior:

Figura 3.7. Altura del jitomate en función de la edad

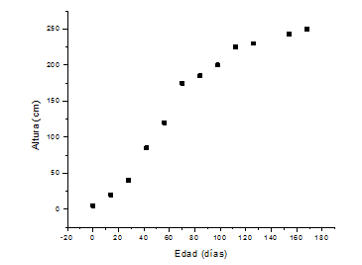
La gráfica nos sugiere que los datos se comportan como un modelo de Gompertz. En consecuencia, para obtener los valores de los coeficientes β_i con i = 1, 2 y 3, es necesario considerar que β_i es la altura máxima que alcanza la planta. En este caso se tiene un valor de 250 cm, aproximadamente.

Para ajustar a una recta los valores de las alturas de la planta en función de su edad, aplicamos la función logaritmo natural dos veces al cociente de la altura máxima alcanzada por la planta entre las diversas alturas (Tabla 3.8).

Tabla 3.8. Datos del ln(ln⁡(β₁/Altura)) en función de la edad

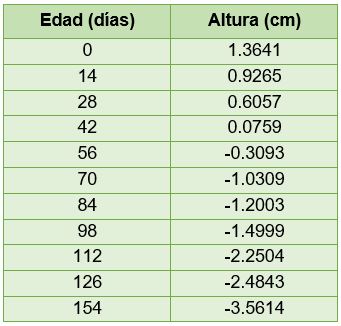
Se calculó el logaritmo natural del cociente de β₁ / Altura = 250 / altura para que al aplicar de nuevo el logaritmo natural a estos resultados, se obtenga una línea recta. La siguiente ecuación muestra este hecho:

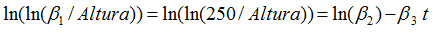
Observa que el último par de datos no aparece porque al calcular por primera vez ln(250/250), el resultado es igual a cero. En consecuencia, al volver a calcular ese logaritmo nos marca error porque no existe el logaritmo natural de 0.

Al calcular por medio del método de mínimos cuadrados, vemos que la pendiente y la ordenada al origen de la recta obtenida son iguales a:

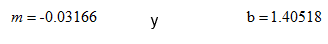
Por lo que concluimos que:

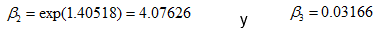
La Figura 3.8 muestra el logaritmo natural del logaritmo natural del cociente de la altura máxima lograda en la planta entre las diversas alturas de ésta.

Figura 3.8. Gráfica de ln(ln⁡(β₁/Altura)) en función de la edad

De esta forma, la ecuación para la altura del jitomate, en función de la edad, está dada por la siguiente expresión:

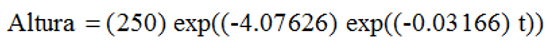
La Tabla 3.9 muestra los valores de la altura de la planta en forma experimental y teórica.

Tabla 3.9. Comparación entre los datos experimentales y los teóricos

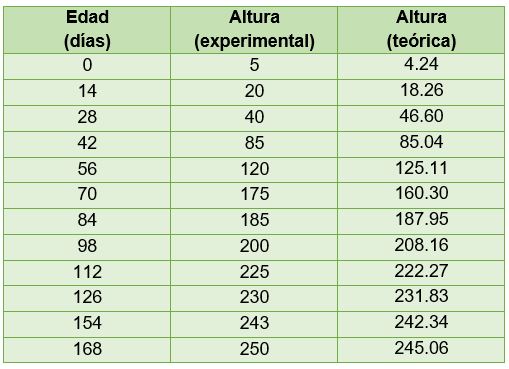
Vemos en la tabla que ambas cantidades son muy similares. Finalmente, el coeficiente de correlación es igual a R = -0.95714368, que es un valor muy cercano a -1. Por lo que se concluye que los datos se asemejan a una relación inversa.

Da clic en el subtema 3.5.2. Modelo de porcentaje de hojas en una planta para revisar el contenido.

Uno de los modelos para el porcentaje de hojas en una planta es el modelo correspondiente con el exponencial. A continuación, en la Tabla 3.10, se muestran los diferentes porcentajes de hojas para diferentes edades.

Tabla 3.10. Datos del porcentaje de hojas en función de la edad

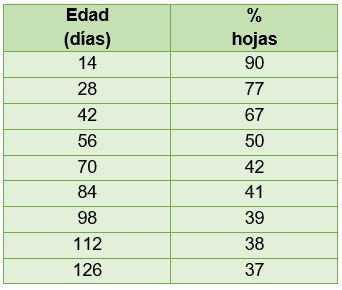
La Figura 3.9 muestra la gráfica del porcentaje de hojas en función de la edad.

Figura 3.9. Porcentaje de hojas en función de la edad

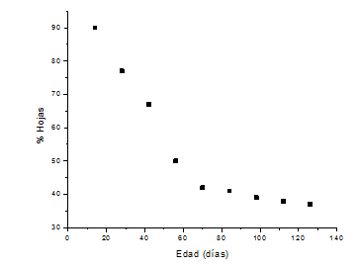
La gráfica nos sugiere que los datos del porcentaje de hojas en función de la edad se comportan como un modelo exponencial. En consecuencia, para obtener los valores de los coeficientes β_i con i = 1, 2 y 3, es necesario considerar que β₁ es el porcentaje mínimo de hojas que tiene la planta. En este caso se tiene un valor del 37%, que corresponde al último día en que se tomaron los porcentajes.

Para ajustar a una recta los valores de los porcentajes de la planta en función de su edad, aplicamos la función logaritmo natural al porcentaje de hojas de la planta menos el porcentaje mínimo registrado de éstas. En este caso, el porcentaje mínimo de hojas registrado es igual a 37%. La Tabla 3.11 muestra la aplicación de la función logaritmo natural:

Tabla 3.11. Datos del ln⁡(% Hojas - 37%) en función de la edad

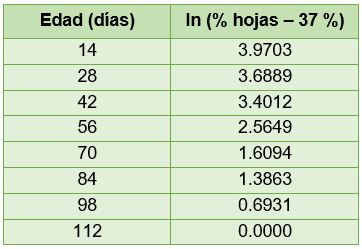
Observa en la tabla que no aparecen los valores correspondientes con el último par de datos, ya que no existe logaritmo de cero. Esto no afecta debido a que se ajustan los datos con los datos que restan.

Se calculó el logaritmo natural de la resta del porcentaje de hojas menos el porcentaje mínimo de hojas para cada edad (% Hojas - 37%), para que se obtenga una línea recta. La siguiente ecuación muestra este hecho:

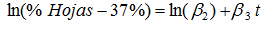
La Figura 3.10 muestra la gráfica de ln(% Hojas - 37%) en función de la edad de la planta.

Figura 3.10. ln(% Hojas - 37%) en función de la edad de la planta

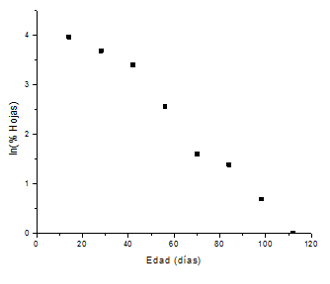
En la figura anterior, observamos que la gráfica se comporta aproximadamente como una línea recta. En consecuencia, al calcular la pendiente y la ordenada al origen por medio del método de mínimos cuadrados, vemos que sus valores son iguales a:

Por lo que concluimos que:

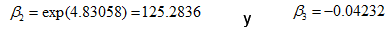
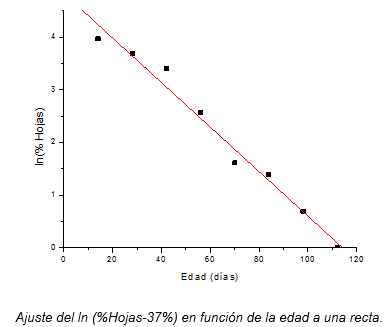
La Figura 3.11 muestra la gráfica del ajuste de los datos a una recta:

Figura 3.11. Ajuste del ln(% Hojas - 37%) en función de la edad a una recta

De esta forma, la ecuación para el porcentaje de hojas en función de la edad está dada por la siguiente expresión:

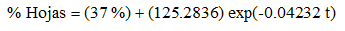
La Tabla 3.12 muestra los valores del porcentaje de hojas en forma experimental y teórica en función de la edad.

Tabla 3.12. Comparación entre los datos experimentales y teóricos

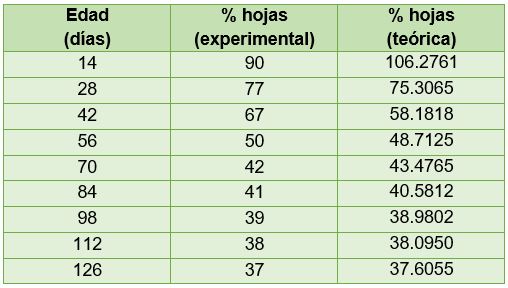
Vemos en la tabla que ambas cantidades son muy similares. Finalmente, el coeficiente de correlación es igual a R = -0.99021, que es un valor muy cercano a -1. En consecuencia, existe una relación muy fuerte de dependencia inversa entre el ln(% Hojas-37%) y la recta.

Da clic en el subtema 3.5.3. Otro modelo de porcentaje de hojas en una planta para revisar el contenido.

Uno de los modelos para el porcentaje de hojas en una planta es el correspondiente con el lineal simple. A continuación, en la Tabla 3.13, se muestran los diferentes porcentajes de hojas para diferentes edades.

Tabla 3.13. Porcentaje de hojas en función de la edad

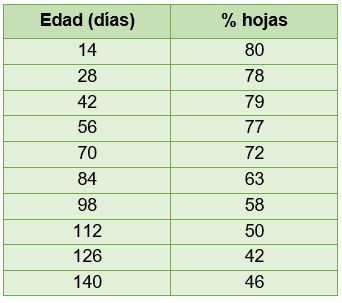
La Figura 3.12 muestra la gráfica con los datos expresados en la tabla.

Figura 3.12. Porcentaje de hojas en función de la edad

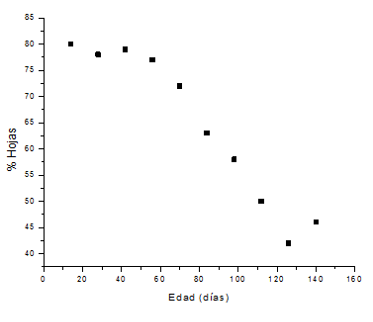
Como se puede observar, podemos considerar que los datos se parecen mucho a una recta. En consecuencia, al calcular la pendiente y la ordenada al origen por medio del método de mínimos cuadrados, vemos que sus valores son iguales a:

Por lo que concluimos que la ecuación de la recta para este conjunto de datos, está dada por:

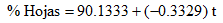
La Figura 3.13 muestra la gráfica del ajuste de los datos a una recta.

Figura 3.13. Ajuste de los datos a una recta

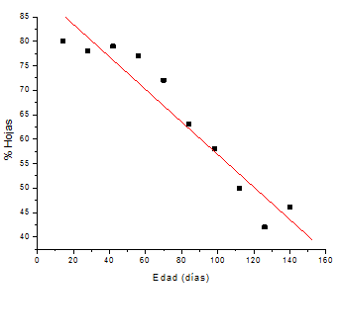
La Tabla 3.14 muestra los valores del porcentaje de hojas en forma experimental y teórica en función de la edad.

Tabla 3.14. Comparación entre los datos experimentales y teóricos

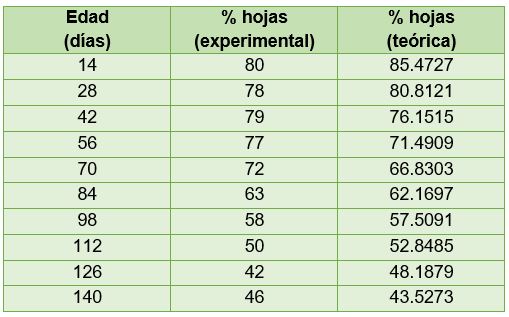
Vemos en la tabla que ambas cantidades son muy similares. Finalmente, el coeficiente de correlación es igual a R = -0.9590, que es un valor muy cercano a -1. En consecuencia, existe una relación muy fuerte de dependencia inversa entre el % Hojas y la recta.

La diferencia en el ajuste de modelos de los porcentajes de hojas es que, en el primer caso, fueron plantas que crecieron en un clima lluvioso, mientras que, en el segundo caso, fueron plantas que crecieron en un clima poco lluvioso. Esto se explica porque biológicamente existe una relación inversa entre el desarrollo y el crecimiento de la planta y su porcentaje de hojas. En el periodo lluvioso este indicador es mayor y más variable.

Asimismo, en el mismo periodo, la proporción de hojas disminuyó de forma exponencial con la edad de la planta, con una gran variabilidad entre edades de corte. Por el contrario, en el periodo poco lluvioso, el porcentaje de hojas también se redujo, pero de forma constante, a ritmo de 0.3329 unidades porcentuales por día.

Es importante aclarar que este modelo empírico no explica la razón por la cual los modelos del porcentaje son diferentes para temporadas de lluvia y temporadas poco lluviosas.

Da clic en la Evidencia de aprendizaje para realizar la actividad.

Da clic en Fuentes de consulta para revisar las fuentes.

Básica

• Blanchard, P., Devaney, R. L., y Hall, G. R. (1999). Ecuaciones Diferenciales. México, D. F.: International Thomson Editores.
• Gil, S. (2014). Experimentos de Física. Buenos Aires, Argentina: Alfaomega.
• Halley, R. J. (1990). Manual de Agricultura y Ganadería. México, D. F.: Noriega LIMUSA.
• Kreyszig, E. (1978). Introducción a la Estadística Matemática, Principios y Métodos. México, D. F.: LIMUSA.
• Mochón, S. (2000). Modelos Matemáticos para Todos los Niveles. México, D.F.: Grupo Editorial Iberoamericana.
• Oda, B. (2007). Introducción al Análisis Gráfico de Datos Experimentales. México, D. F.: UNAM.

Complementaria

• De Torres Curth, M. (2015). Los reyes de la pasarela, modelos matemáticos en las ciencias. Buenos Aires, Argentina: Fundación de Historia Natural Félix de Azara.