En la primera y la segunda unidad aprendiste a utilizar los principios de ecuaciones diferenciales para resolver una ecuación diferencial ordinaria mediante varias técnicas de derivación y, también, a utilizar métodos algebraicos para resolver ecuaciones diferenciales lineales por medio de una ecuación característica. En esta tercera, unidad, aprenderás a utilizar las propiedades de la Transformada de Laplace para determinar una ecuación diferencial en un problema algebraico mediante las operaciones de derivación.

¿Para qué necesitamos la Transformada de Laplace?

Si analizamos el comportamiento dinámico de algunos procesos en la vida cotidiana (por ejemplo: controlar temperatura y humedad en un edificio, o el análisis de la suspensión de un automóvil) puede representarse de manera aproximada por el siguiente modelo general de comportamiento dinámico lineal:

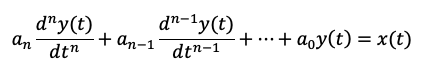
La transformada de Laplace es una herramienta matemática muy útil para el análisis de sistemas dinámicos lineales; por ejemplo: en la transportación para controlar el movimiento de un vehículo de un lugar a otro de manera segura, o en la industria, para controlar el proceso de manufactura. Además, permite resolver ecuaciones diferenciales lineales mediante una transformación en ecuaciones algebraicas y es una herramienta muy útil para resolver problemas que generan ecuaciones diferenciales muy complejas, que a menudo son difíciles de resolver. Este tipo de ecuaciones se origina durante el estudio de circuitos electrónicos, circuitos eléctricos y sistemas de control.

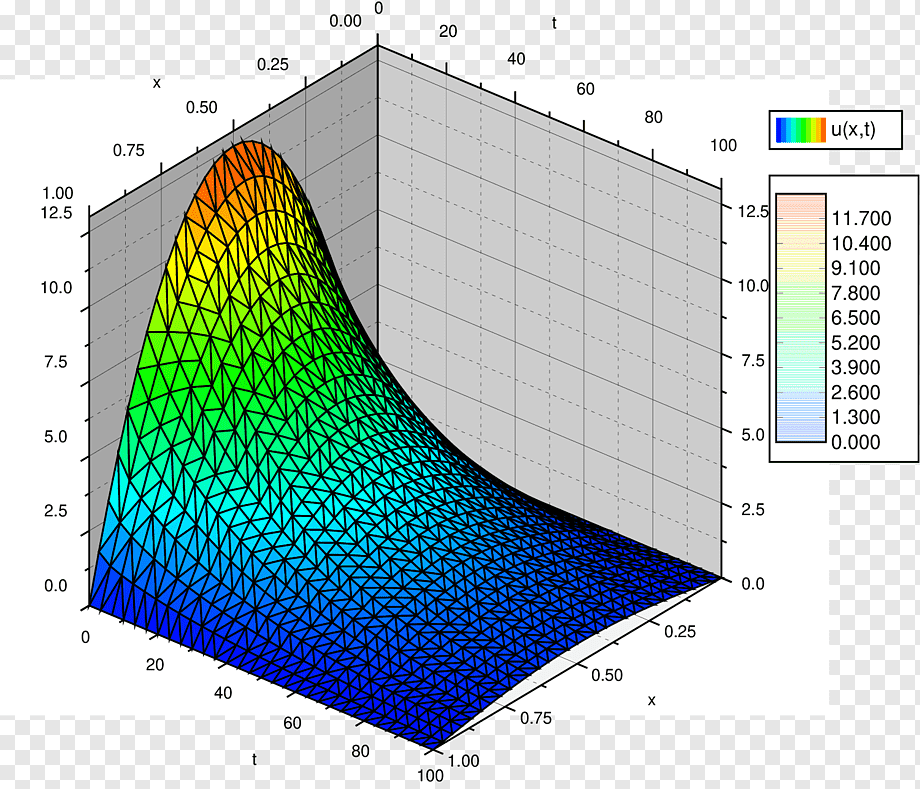
Fuente: Imagen extraída de https://n9.cl/8ehqb

Da clic en Competencias para continuar el estudio de la unidad 3.