Bienvenida
Para desarrollar la teoría de integrabilidad es indispensable definir la integral de Lebesgue para funciones medible no negativas, así como establecer unas de sus propiedades fundamentales. Además de hacer la comparación con la integral de Riemann. Observarás que la colección de funciones semicontinuas superiormente es un espacio de funciones y este conjunto son las funciones Lebesgue integrables.
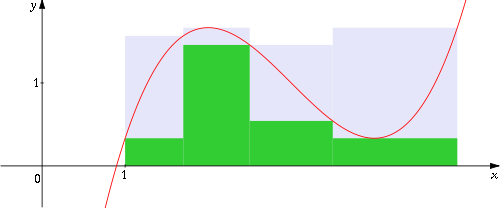
Fuente: Imagen extraída de https://n9.cl/q55rre
Da clic en Competencias para continuar el estudio de la unidad 4.
Competencia específica
Aplicar el concepto de integral de Lebesgue para calcular integrales sobre dominios no tradicionales mediante la identificación de sus características.
Logros
- Definir la integral de Lebesgue.
- Comparar la integral de Lebesgue con los conceptos previos de medida y de integral de Riemann.
- Establecer propiedades básicas de la integral de Lebesgue.
Da clic en Contenido para continuar el estudio de la unidad 4.
Contenido
Material de estudio
Da clic en el ícono, para descargar el contenido de la Unidad 4.
Da clic en Cierre para continuar el estudio de la Unidad 4.
Cierre
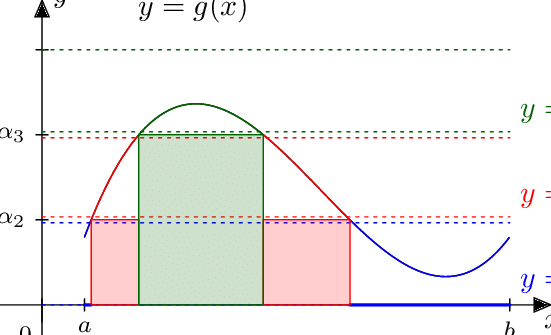
Fuente: Imagen extraída de https://n9.cl/5zk2z
La integral de Lebesgue es de alguna forma la generalización natural del concepto de integral de funciones medibles en los conjuntos medibles. Una importancia fundamental es la que se manifiesta en Lema de Fatou: que argumenta la monotonía de la integral bajo sucesiones de funciones medibles. El contenido de esta unidad es fundamental para el desarrollo de la Teoría de Integración que es una de las ramas más importantes de la matemática con una aplicación directa en la estadística y probabilidad. El dominio de esta unidad didáctica permitirá al estudiante la resolución de problemas planteados en ecuaciones diferenciales ordinarias y parciales con un entendimiento profundo de las propiedades y teoremas involucrados en la obtención de tales resultados.
Da clic en Fuentes de consulta para concluir el estudio de la Unidad 4.
Fuentes de consulta
Básica
- Charalambos A.D. (1998). Principles of Real Analysis. USA: Academic Press.
- De Barra, G. (2000). Measure Theory and Integration. India: New Age International.
- Folland, G. (1999). Real Analysis: Modern Techniques and their Applications. USA: Wiley.
- Galaz, F. (2002). Medida e Integral de Lebesgue en .México: University Press.
- Grabisnky, G. (2011). Teoría de la Medida. México: Facultad de Ciencias UNAM.
- Halmos, P. (1991). Measure Theory. USA: Springer Verlag.
- Hawkins T. (1970) Lebesgue theory of integration. Its origins and development: Chelsea Publishing Company.
- Royden, H; Fitzpatrick, P. (2010). Real Analysis. USA: Pearson.
- Sánchez, C. C. (2004). De los Bernoulli a los Bourbaki. España: Nivola.
- Schram, M. (1996). Introduction to Real Analysis. USA: Prentice Hall.
Muy bien, has concluido el estudio de la Unidad 4, ahora realiza las Actividades de aprendizaje.