Bienvenida
En la unidad 1 hemos visto el teorema fundamental del cálculo, el cual menciona que es posible integrar una función si conocemos su antiderivada, o su integral definida. También hemos adquirido habilidad para resolver cierto tipo de integrales; sin embargo, existen integrales más complicadas que no es posible resolverlas con las fórmulas y métodos hasta ahora expuestos. Por ello, en este capítulo abordaremos diferentes técnicas y métodos para resolver integrales.
Entre los métodos que veremos están integración por partes, integración usando funciones trigonométricas, integraciones por sustitución trigonométrica, integración de un cociente mediante la descomposición de fracciones parciales entre sus diferentes casos. También veremos el cómo abordar cierto tipo de integrales mediante tablas y/o aplicando algunas estrategias para realizar el proceso de integración con éxito. Incluso abordaremos las integrales impropias en donde extenderemos el concepto de integral definida al caso donde el intervalo es infinito y también al caso donde f tiene una discontinuidad infinita en un intervalo [a, b].
Universidad de La Laguna. (s.f.). Imagen sobre cálculo integral [Imagen]. https://campusvirtual.ull.es/ocw/mod/page/view.php?id=3460
Da clic en Competencias para continuar el estudio de la unidad 3.
Competencia específica
Utilizar métodos de integración para resolver integrales mediante reglas, identidades, sustituciones, simplificaciones, definiciones, estrategias y tablas, con base en ejercicios de práctica.
Logros
- Proponer diversos métodos de investigación.
- Determinar el valor del área de diferentes cuerpos curvos.
- Resolver ejercicios relacionados con integrales trigonométricas.
- Resolver ejercicios relacionados con integrales impropias.
- Resolver problemas que presenten argumentos sobre integrales.
Da clic en Contenido para continuar el estudio de la unidad 3.
Contenido
Material de estudio
Da clic en el ícono, para descargar el contenido de la unidad 3.
Material de apoyo
Da clic en el ícono, para descargar el material de apoyo.
Da clic en Cierre para continuar el estudio de la unidad 3.
Cierre
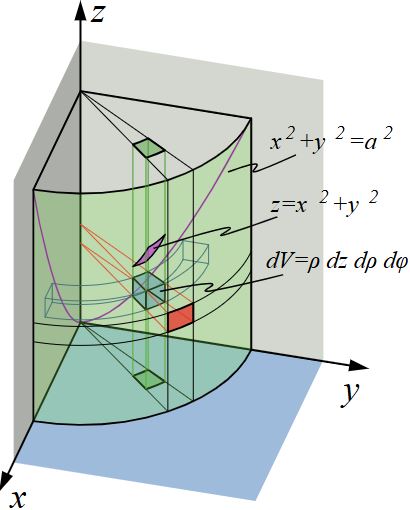
Inductiveload. (2008, 8 de junio). Triple Integral Example [Imagen]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Triple_Integral_Example.svg
La unidad didáctica brinda las habilidades necesarias para aplicar las herramientas matemáticas en unidades didácticas posteriores, principalmente en la resolución de problemas de cálculo para satisfacer las necesidades de áreas afines como pueden ser las siguientes carreras: Telemática, Desarrollo de Software, Logística y Transporte, Biotecnología, Tecnología ambiental y Energías renovables.
Da clic en Fuentes de consulta para concluir el estudio de la unidad 3.
Fuentes de consulta
Básica
- Apostol, T. M. (2008). Calculus. España: Reverté.
- Larson, R. E. (2005). Cálculo. México: Mc Graw Hill.
- Leithold, L. (2009). El Cálculo. México: Oxford University Press.
- Stewart, James. (2008). Cálculo. Trascendentes tempranas. México: Cengage Learning.
Muy bien, has concluido el estudio de la unidad 3, ahora realiza las Actividades de aprendizaje.