Bienvenida
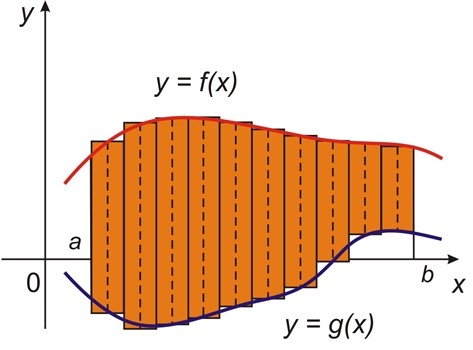
En esta unidad trataremos el caso de cómo calcular áreas limitadas por dos funciones, veremos que estos métodos tienen mucho que ver con el primer capítulo, donde analizamos la suma de Riemann para integración de ciertas áreas. De manera análoga utilizaremos el concepto de sumas de Riemann para llegar a la integral definida, útil para calcular el área entre dos curvas de funciones, limitadas al intervalo [a, b].
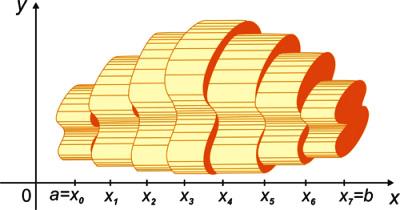
Veremos también los métodos de integración para calcular volúmenes de sólidos. Para ello revisaremos el concepto de volumen, que nos será de gran utilidad para tener la idea intuitiva de lo que es volumen. Calcularemos volúmenes usando los métodos de sólido de revolución y el método de cálculo de volúmenes mediante cascarones esféricos. Por otra parte, comprenderemos lo que es un valor medio de una función y el valor promedio de una función.
Competencia específica
Analizar problemas modelo para calcular áreas entre curvas, volúmenes, así como el valor promedio de una función mediante el uso de aproximaciones, con base en definiciones, métodos y teoremas.
Logros
- Resolver ejercicios usando la regla de integración por partes.
- Emplear métodos de integración.
- Calcular integrales.
- Usar las tablas de integrales.
Cierre
En esta sección requerimos el siguiente material:
- Calculadora.
- Tablas de integración. Existen libros en las bibliotecas que podrías utilizar o bien adquirir las tablas de Internet. Te aconsejamos que lleves contigo las tablas para evaluar las integrales.
- Es necesario que repases las fórmulas para encontrar áreas de figuras geométricas planas y volumétricas comunes.
Es necesario que tengas conocimientos sobre:
- Álgebra
- Geometría analítica
- Cálculo diferencial
- Propiedades y reglas de las operaciones de sumatorias.
Fuentes de consulta
Básica
- Apostol, T. M. (2008). Calculus. Reverté
- Larson, R. E. (2005). Cálculo. McGraw Hill.
- Leithold, L. (2009). El Cálculo. Oxford University Press
- Stewart, James. (2008). Cálculo. Trascendentes tempranas. Cengage Learning.